安全工程专业课程
矿山压力与岩层控制
金洪伟 & 双海清
安全科学与工程学院
如何浏览?
- 从浏览器地址栏打开 https://zimo.net/ky/;
- 点击链接打开演示文稿,使用空格键或方向键导航;
- 按f键进入全屏播放,再按Esc键退出全屏;
- 按s键打开演讲者视图(在多屏播放时有用);
- 按Alt键同时点击鼠标左键进行局部缩放;
- 按Esc或o键进入幻灯片浏览视图。
请使用最新版本浏览器访问此演示文稿以获得更好体验。
第二章 矿山岩体的原岩应力及其重新分布
目 录
第一节 岩体中的原岩应力
第一节 岩体中的原岩应力
一、自重应力
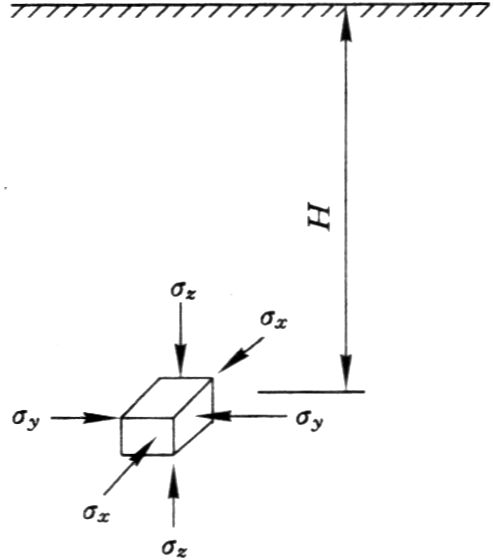
设岩体为半无限体,地面为水平面,在距地表深度为 H 处任意取一单元体,其上作用的应力为 \({\sigma _z}\)、\({\sigma _y}\)、\({\sigma _x}\),则有
\[\left. \begin{array}{l} {\sigma _z} = \gamma H\\ {\sigma _x} = {\sigma _y} = \lambda {\sigma _z}\\ {\tau _{xy}} = 0 \end{array} \right\}\]
式中,λ 为侧压系数。
一、自重应力
根据广义胡克定律
\[\left. \begin{array}{l} {\varepsilon _z} = \frac{1}{E}\left[ {{\sigma _z} - \mu \left( {{\sigma _x} + {\sigma _y}} \right)} \right]\\ {\varepsilon _x} = \frac{1}{E}\left[ {{\sigma _x} - \mu \left( {{\sigma _y} + {\sigma _z}} \right)} \right]\\ {\varepsilon _y} = \frac{1}{E}\left[ {{\sigma _y} - \mu \left( {{\sigma _x} + {\sigma _z}} \right)} \right] \end{array} \right\}\]
由于 \({\varepsilon _x}\)=0,\({\varepsilon _y}\)=0,可得:
\[\lambda = \frac{\mu }{{1 - \mu }}\]
岩石的泊松比 μ 一般为 0.2~0.3,侧压系数 λ 等于 0.25~0.43。
一、自重应力
分布规律:
- 岩体的垂直方向的自重应力 σz 随深度呈线性增长。
- 在一定的深度范围内,岩体基本上处于弹性状态。
- 当埋深超过一定深度时,自重应力大于岩体的弹性强度,岩体将转化为潜塑性状态或塑性状态,且有 σz=σx=σy=γH。
第一节 岩体中的原岩应力
二、构造应力
构造应力是由于地壳构造运动在岩体中引起的应力,可分为现代构造应力和地质构造残余应力。其特点为:
- 主要是水平压应力;
- 具有明显的区域性:随地质构造剧烈程度而产生较大的变化;
- 具有明显的方向性:最大水平主应力和最小水平主应力相差较大;
- 多出现在坚硬岩层中。
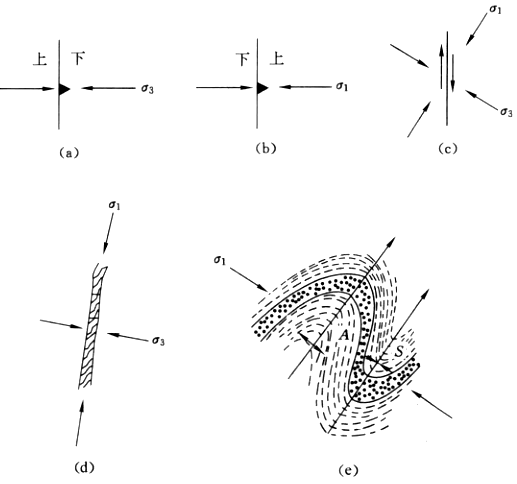
(a)正断层;(b)逆断层;(c)平移断层;(d)岩脉;(e)褶皱
第一节 岩体中的原岩应力
三、原岩应力分布的基本规律
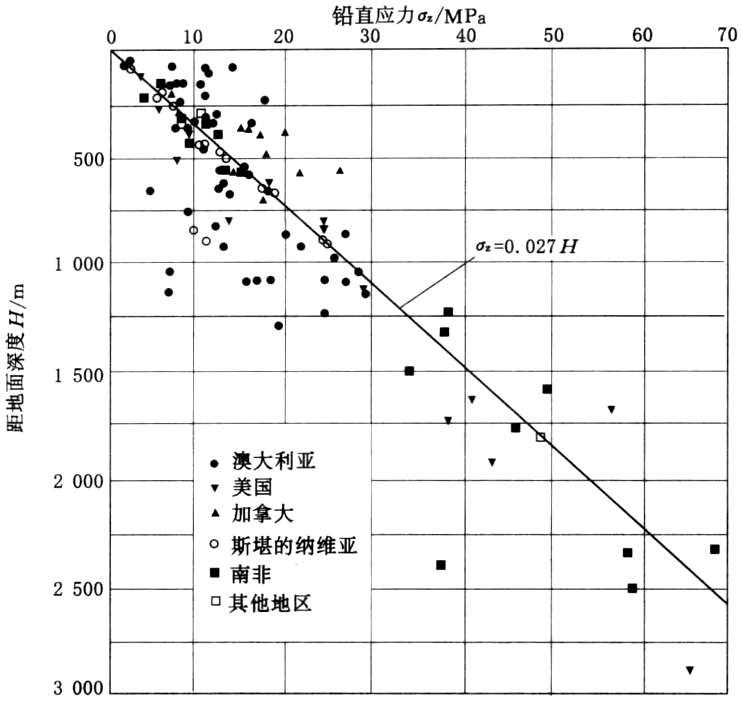
- 实测铅直应力基本上等于上覆岩层重量。见下页图。
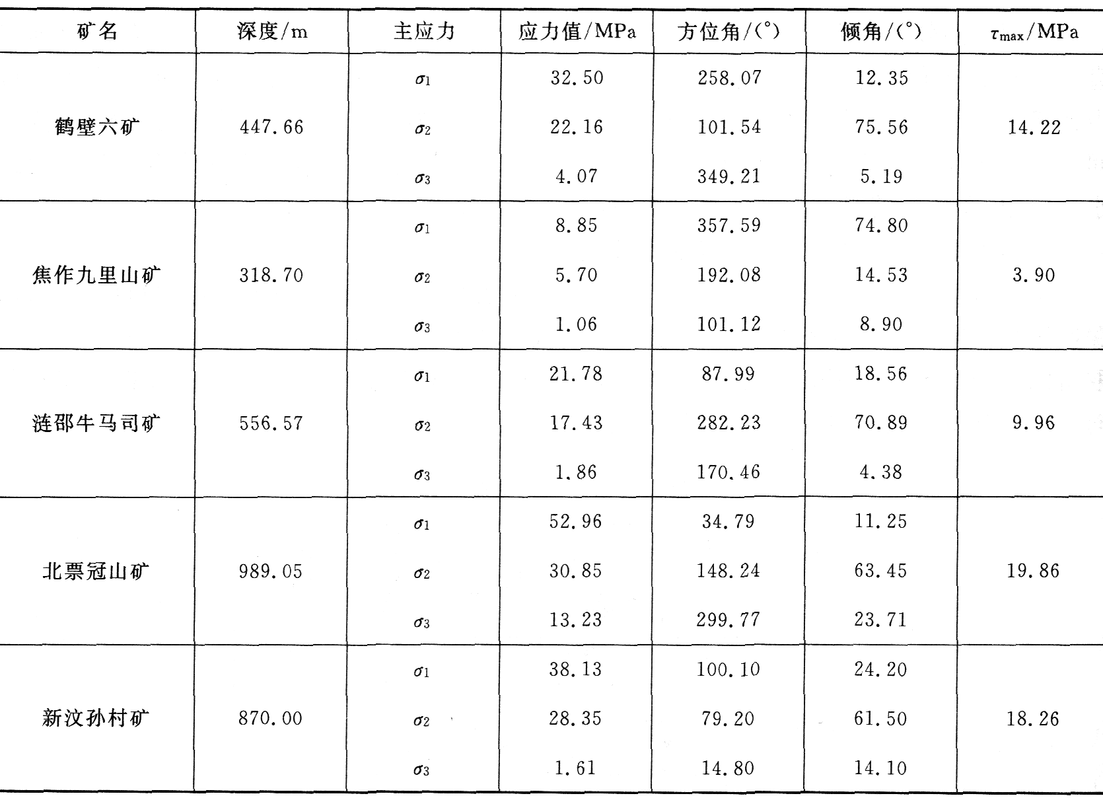
- 水平应力普遍大于铅直应力。最大水平应力 σh, max 与铅直应力 σz 的比值一般为 0.5~5.5,很多情况下比值大于 2。
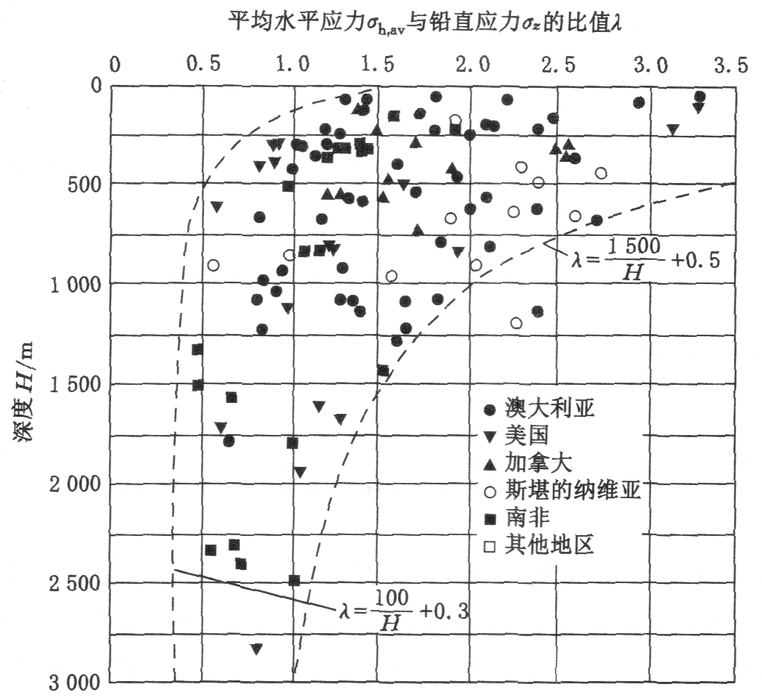
- 平均水平应力与铅直应力的比值随深度增加而减小。浅部侧压系数大,为 2 左右,且其值比较分散;深度增加侧压系数减小,趋向于 1。见下下页图。
- 最大水平主应力和最小水平主应力一般相差较大。
σh, min/σh, max 一般为 0.2~0.8,多数情况下为 0.4~0.8。
第二节 “孔”周围的应力分布
为了求得巷道及其他回采空间周围的应力分布,对巷道形状、围岩性质、载荷分布等做一系列简化假设,求得最简单条件下的应力分布规律。
- 不同的侧压系数 λ;
- 不同的孔的形状:圆形、椭圆形、矩形等;
- 岩性:均质的连续体;
- 忽略巷道影响范围(3~5 倍的巷道半径 R0)内的岩石自重。
第二节 “孔”周围的应力分布
一、双向等压应力场内的圆形孔
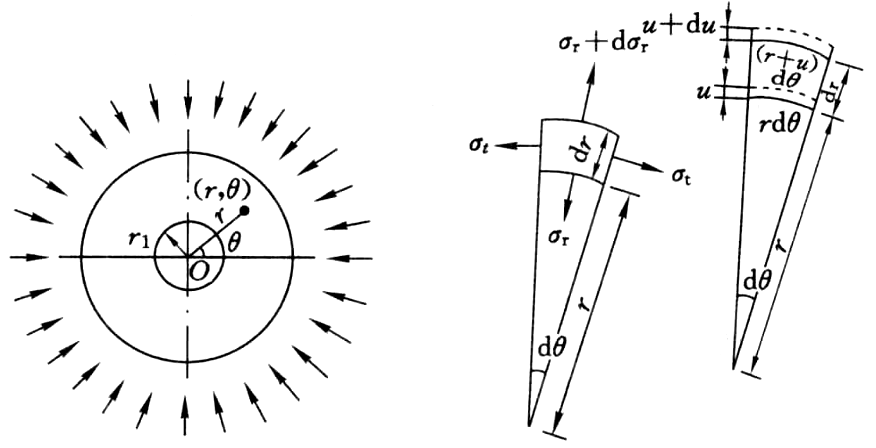
一、双向等压应力场内的圆形孔
所求解问题可简化为平面应变问题,分别建立极坐标系下的平衡方程、几何方程和本构方程,联立求解得:
\[{\sigma _r} = \gamma H\left( {1 - \frac{{r_1^2}}{{{r^2}}}} \right)\]
\[{\sigma _t} = \gamma H\left( {1 + \frac{{r_1^2}}{{{r^2}}}} \right)\]
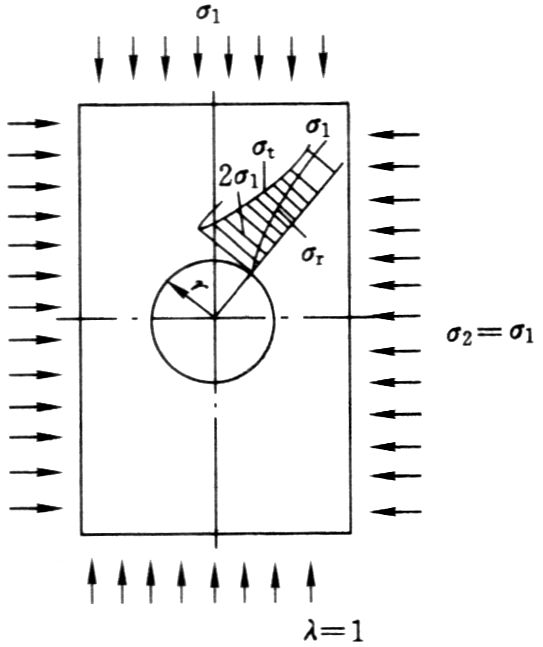
讨论:
- 圆孔周边全处于压缩应力状态。
- 应力大小与弹性常数 E、μ 无关。
- σt 和 σr 的分布与角度无关,皆为主应力。
- 孔周边的切向应力为最大应力,最大应力集中系数 K=2,且与孔径的大小无关。
- 其他各点的应力大小与孔径有关。若定义以 σt>1.05σ1或σr<0.95σ1 为巷道影响圈的边界,则 σt 的影响半径 \({R_t} = \sqrt {20} {r_1} \approx 5{r_1}\),工程上有时以 10% 作为影响半径,则 σt 的影响半径 \({R_t} \approx 3{r_1}\)。有限元计算常取 5r1 的范围作为计算域。
- 圆孔周围任意点的切向应力 σt 与径向应力 σr 之和为常数,且等于 2σ1。
第二节 “孔”周围的应力分布
二、双向不等压应力场内的圆形孔
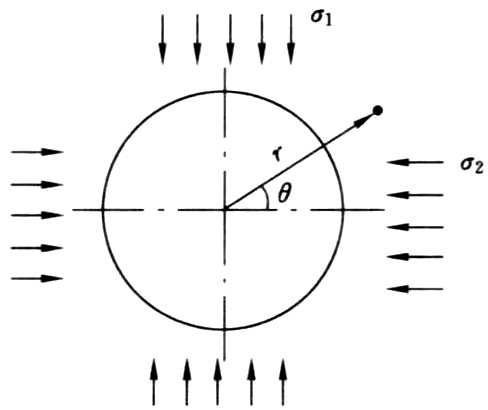
求解方法与前面类似,所得结果为:
\[{\sigma _r} = \frac{{\gamma H}}{2}\left( {1 + \lambda } \right)\left( {1 - \frac{{r_1^2}}{{{r^2}}}} \right) - \frac{{\gamma H}}{2}\left( {1 - \lambda } \right)\left( {1 - 4\frac{{r_1^2}}{{{r^2}}} + 3\frac{{r_1^4}}{{{r^4}}}} \right)\text{cos} 2\theta \]
\[{\sigma _t} = \frac{{\gamma H}}{2}\left( {1 + \lambda } \right)\left( {1 + \frac{{r_1^2}}{{{r^2}}}} \right) - \frac{{\gamma H}}{2}\left( {1 - \lambda } \right)\left( {1 + 3\frac{{r_1^4}}{{{r^4}}}} \right)\text{cos} 2\theta \]
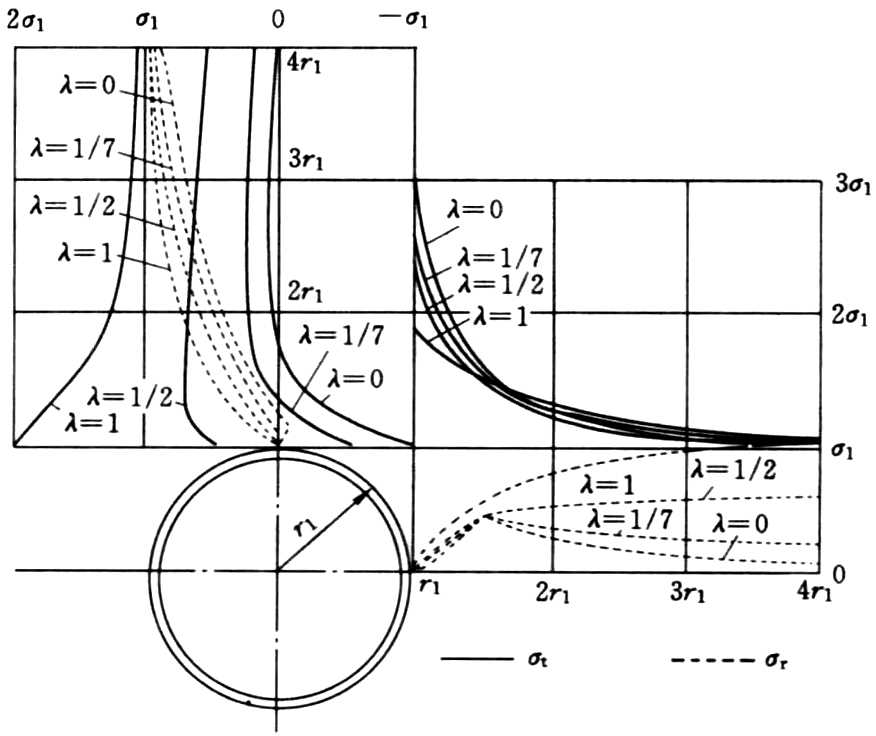
规律总结:
- 0≤λ<1/3 时,孔周边上下位置出现拉应力,拉应力在 θ=90°和 θ=270° 处达到最大值;λ>1/3 时,孔周边不出现拉应力。
- λ=0 时,在 θ=90° 和 270° 处,出现最大拉应力,值为 -σ1;在 θ=0° 和 180° 处,出现最大压应力,集中系数为 3。
- 0≤λ<1 时,孔周边最大压应力集中位置出现在左右两侧;λ>1 时,最大压应力集中位置出现在上下位置。
所以,λ=0 为最不利情况;λ=1 为均匀受压的最有利于稳定的情况。
第二节 “孔”周围的应力分布
三、椭圆形孔周边的应力分布
在一般原岩应力状态下,深埋椭圆巷道周边切向应力计算公式为:
\[\begin{array}{c} {\sigma _\theta } = {p_0}\frac{{{m^2}{{\text{sin} }^2}\theta + 2m{{\text{sin} }^2}\theta - {{\text{cos} }^2}\theta }}{{{{\text{cos} }^2}\theta + {m^2}{{\text{sin} }^2}\theta }} + \\ \lambda {p_0}\frac{{{{\text{cos} }^2}\theta + 2m{{\text{cos} }^2}\theta - {m^2}{{\text{sin} }^2}\theta }}{{{{\text{cos} }^2}\theta + {m^2}{{\text{sin} }^2}\theta }} \end{array}\]
式中,m=b/a。
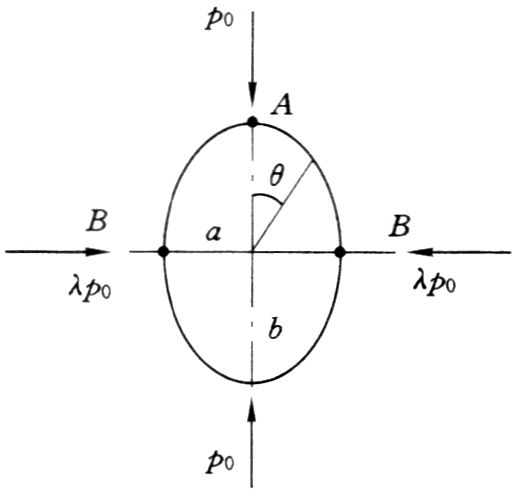
三、椭圆形孔周边的应力分布
(1)等应力轴比
等应力轴比就是使巷道周边应力均匀分布时的椭圆长短轴之比。由 \({\text{d}}{\sigma _\theta }/{\text{d}}\theta = 0\),得:
\[m = \frac{1}{\lambda }\]
将此 m 值代入上页 σθ 求解式得:
\[{\sigma _\theta } = {p_0} + \lambda {p_0}\]
等应力轴比对地下工程的稳定是最有利的。
(1)等应力轴比
- λ=1 时,m=1,a=b,最佳断面为圆形;
- λ=1/2 时,m=2,2a=b,最佳断面为 2a=b 的竖椭圆;
- λ=2 时,m=1/2,a=2b,最佳断面为 a=2b 的横(卧)椭圆。
椭圆长轴总是顺着原岩应力的最大主应力的方向,且满足等应力轴比,对地下工程的稳定最为有利。
三、椭圆形孔周边的应力分布
(2)零应力(无拉应力)轴比
当不能满足最佳轴比时,可以退而求其次。岩体抗拉强度最弱,找出满足不出现拉应力的轴比,即零应力(无拉应力)轴比。(解算过程略)
第二节 “孔”周围的应力分布
四、矩形孔和其他形状巷道周边的应力分布
- 计算复杂,无法通过解析法计算。
- 在弹性应力条件下,巷道断面围岩中的最大应力是周边的切向应力,且周边应力大小和 E、μ 弹性参数无关。
- 应力分布和原岩应力场分布(大小)、巷道的形状(竖向和横向轴比)有很大关系。
- 断面在拐角的地方应力发生急剧变化,在直长边则容易出现拉应力。
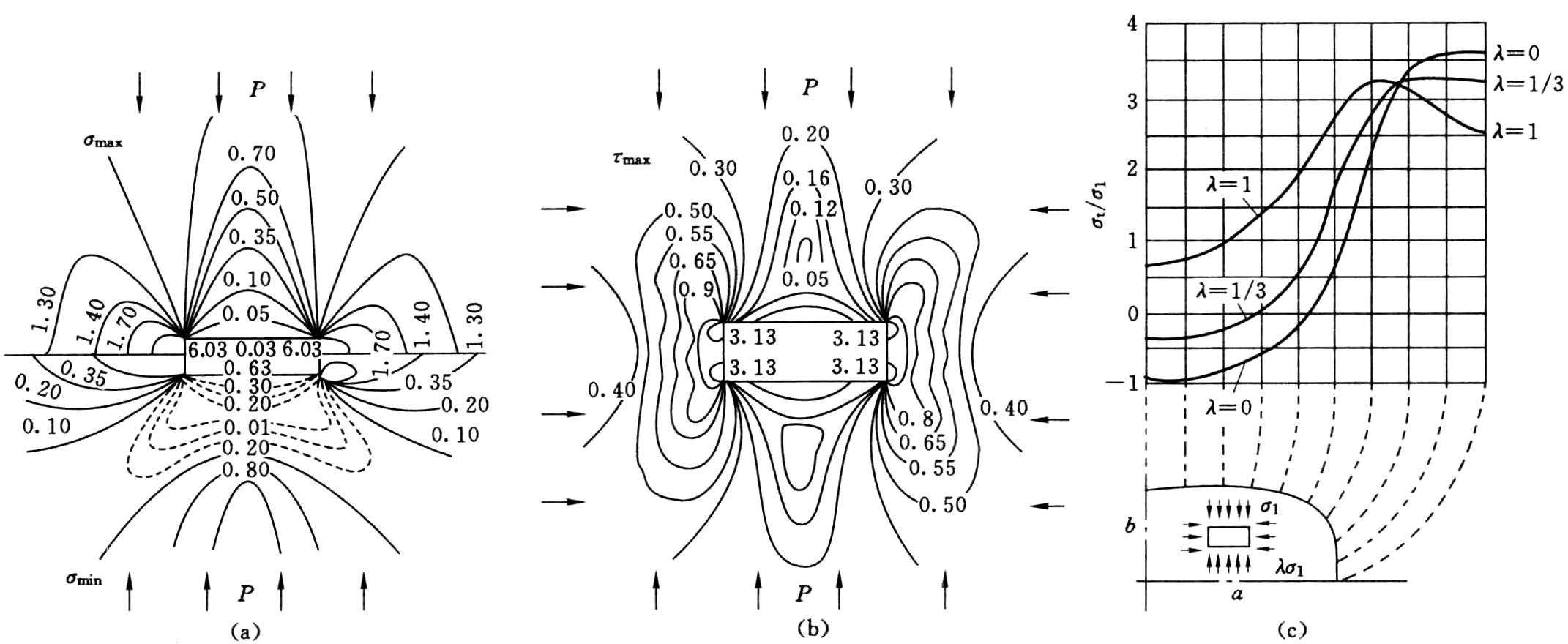
(a)正应力;(b)剪应力(切向应力);(c)周边切向应力
第二节 “孔”周围的应力分布
五、多孔周围的应力分布
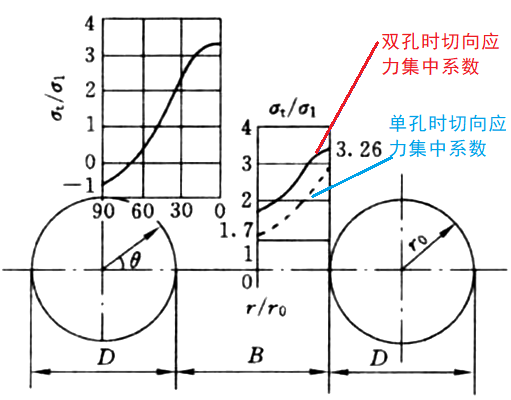
时的切向应力分布图
双孔相互影响,应力集中程度更高
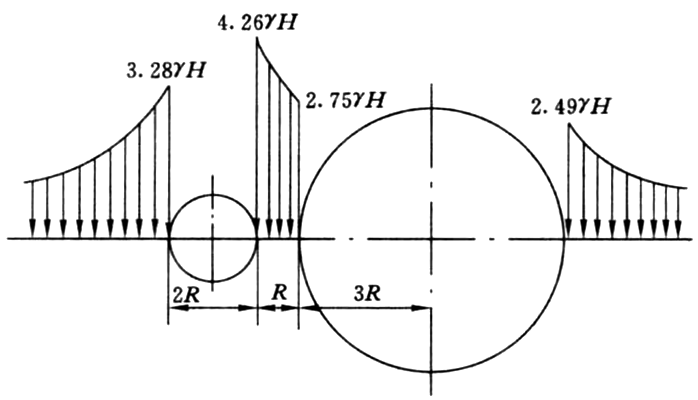
的切向应力分布图
大孔对小孔的影响高于
小孔对大孔的影响
五、多孔周围的应力分布
相邻两孔的影响程度及多孔周围的应力分布受到下列一些因素的影响:
- 孔断面的形状及其尺寸大小;
- 相邻两孔间的距离;
- 在同一水平内相邻孔的数目;
- 原岩应力场的性质和有关参数。
第二节 “孔”周围的应力分布
综上所述,在假设孔周围都处于弹性状态的条件下,应力重新分布有以下一些特点:
- 孔周围形成了切向应力集中,最大切向应力发生在孔的周边;
- 应力集中系数 k 的大小,与侧压系数 λ、椭圆孔轴长比 m、多孔应力叠加情况有关;
- 应力重新分布的影响区从理论上来说是无限的,但通常可取切向应力的值超过原岩铅直应力 5% 处作为边界线;
- 孔的影响范围与孔的断面大小有关,断面越大,影响范围也越大。
第三节 围岩的极限平衡与支承压力分布
- 支承压力
- 在岩体内开掘巷道后,巷道围岩必然出现应力重新分布,一般将巷道两侧改变后的切向应力增高部分称为支承压力(abutment pressure)(
支撑压力×)。
支承压力是矿山压力的重要组成部分,一般巷道两侧的应力集中系数为 2~3。
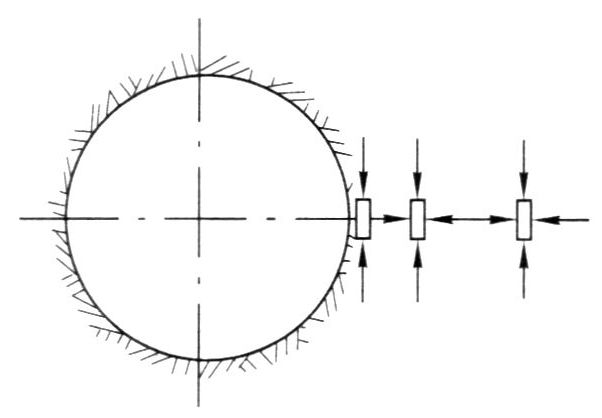
第三节 围岩的极限平衡与支承压力分布
巷道周边的岩块侧向(径向)应力为零,为单向压缩状态,随着向岩体深部发展,岩块逐渐变为三向应力状态。
若巷道两侧是松软岩层,如煤、页岩等,则在此压力作用下就可能处于破坏状态。随着破坏向岩体内部发展,岩块因处于三向应力状态而抗压强度增加,直到某一半径R处岩块又处于弹性状态。这样半径 R 范围内的岩体就处于极限平衡状态(破坏状态、塑性状态),这个范围称为极限平衡区。
第三节 围岩的极限平衡与支承压力分布
求解方法:
在极坐标系或笛卡尔坐标系中取微元体,列出其平衡方程并化简,同时在极限平衡区内岩石符合莫尔-库伦准则,给定巷道(孔)内壁的支架反作用力(径向力,无支护时为零)边界条件,联立求得巷道周围径向、切向(或垂直、水平方向)的应力分布。
再利用一些方法得出支承压力极限平衡区边界处的最大集中应力,进而求得极限平衡区半径 R。
第三节 围岩的极限平衡与支承压力分布
1. 圆形孔周围的应力分布
\[{\sigma _r} = C\cot \varphi \left[ {{{\left( {\frac{r}{{{r_1}}}} \right)}^{\frac{{2\text{sin} \varphi }}{{1 - \text{sin} \varphi }}}} - 1} \right]\]
\[{\sigma _t} = C\cot \varphi \left[ {\frac{{1 + \text{sin} \varphi }}{{1 - \text{sin} \varphi }}{{\left( {\frac{r}{{{r_1}}}} \right)}^{\frac{{2\text{sin} \varphi }}{{1 - \text{sin} \varphi }}}} - 1} \right]\]
\[R = {r_1}{\left[ {\frac{{\left( {\gamma H + C\cot \varphi } \right)\left( {1 - \text{sin} \varphi } \right)}}{{C\cot \varphi }}} \right]^{\frac{{1 - \text{sin} \varphi }}{{2\text{sin} \varphi }}}}\]
1. 圆形孔周围的应力分布
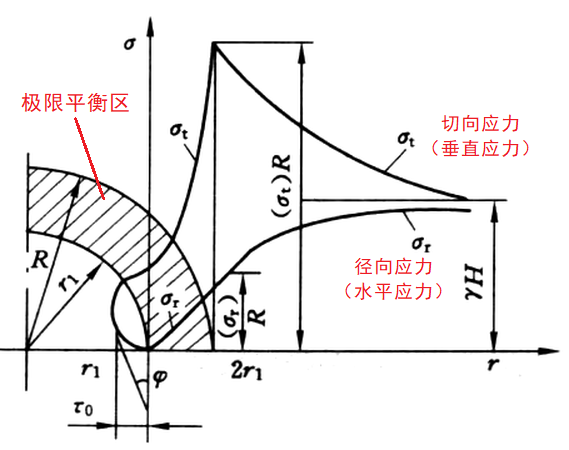
2. 采场前方支承压力分布
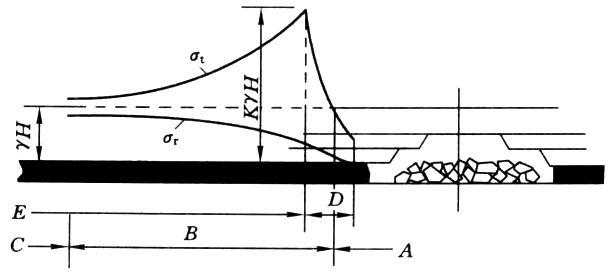
A—减压区;B—增压区;C—稳压区;
D—极限平衡区;E—弹性区
第四节 支承压力在底板岩层中的传播
首先求在集中力 P 作用下,半无限平面内的应力分布。然后可用积分形式解决其他形式载荷条件下的应力分布问题。
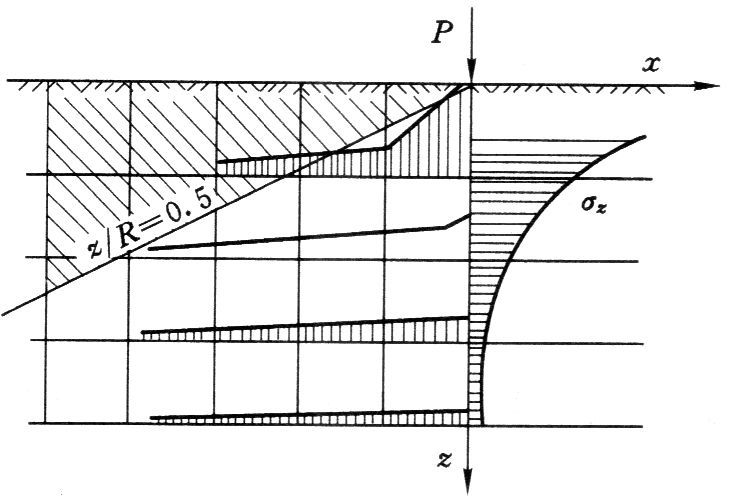
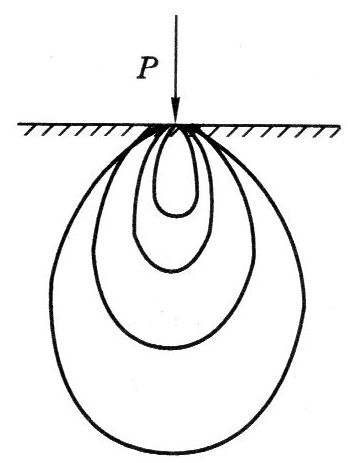

(a)煤柱下的 σz 应力等值线;(b)煤体下的 σz 应力等值线
学习要求
- 了解原岩应力的分类。
- 掌握自重应力的计算方法。
- 掌握原岩应力分布的基本规律。
- 掌握弹性应变能和应变能密度的概念,理解应变能密度的计算公式(式2-18和式2-19)。
- 掌握线弹性条件下,侧压系数为1时圆形孔洞周围的应力分布规律(式2-32和式2-33及相关解释)。
- 了解不同侧压系数条件下,圆形孔洞周围的应力分布规律(看懂图2-13,并理解其分布规律)。
- 掌握等应力轴比的概念以及λ分别等于1、1/2和2时最合适的巷道形状(掌握式2-39)。
- 掌握支承压力和极限平衡区的概念。
- 了解巷道两侧支承压力分布特征(看懂图2-23,掌握图2-25的各分区名称)。
作 业
- 课本69页习题3:试述原岩应力分布的基本特点。
- 课本69页习题5:计算赋存深度为 600m 处的圆形水平巷道的最大切向压应力与切向拉应力。令岩层的平均体积力为25kN/m3,泊松比μ=0.2,弹性模量E=250MPa。
- 课本69页习题6:试绘制λ=1/3时圆形水平巷道周围的应力重新分布图,并叙述其特点。
- 课本69页习题9:试分析支承压力的有利因素与不利因素。