安全工程专业课程
矿山压力与岩层控制
金洪伟 & 双海清
安全科学与工程学院
如何浏览?
- 从浏览器地址栏打开 https://zimo.net/ky/;
- 点击链接打开演示文稿,使用空格键或方向键导航;
- 按f键进入全屏播放,再按Esc键退出全屏;
- 按s键打开演讲者视图(在多屏播放时有用);
- 按Alt键同时点击鼠标左键进行局部缩放;
- 按Esc或o键进入幻灯片浏览视图。
请使用最新版本浏览器访问此演示文稿以获得更好体验。
第一章 矿山岩石和岩体的基本性质
目 录
第一节 岩石的基本物理性质
一、岩石的基本概念
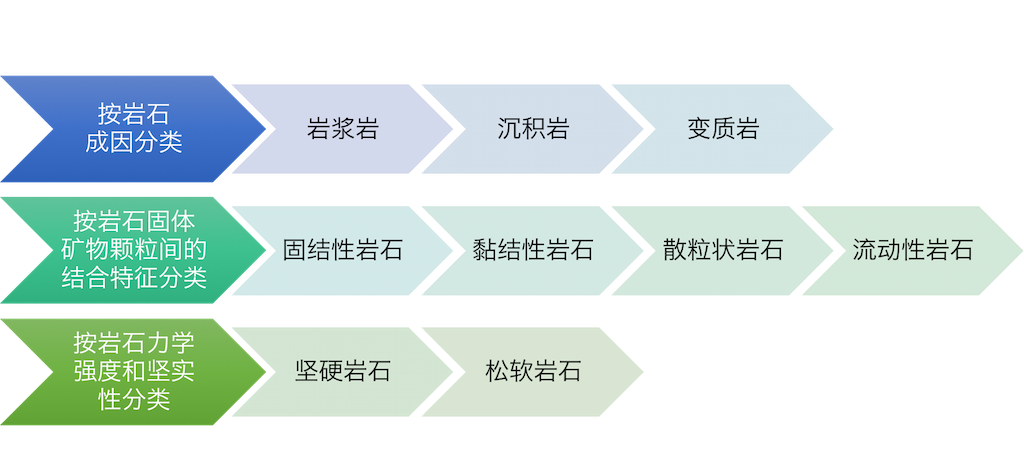
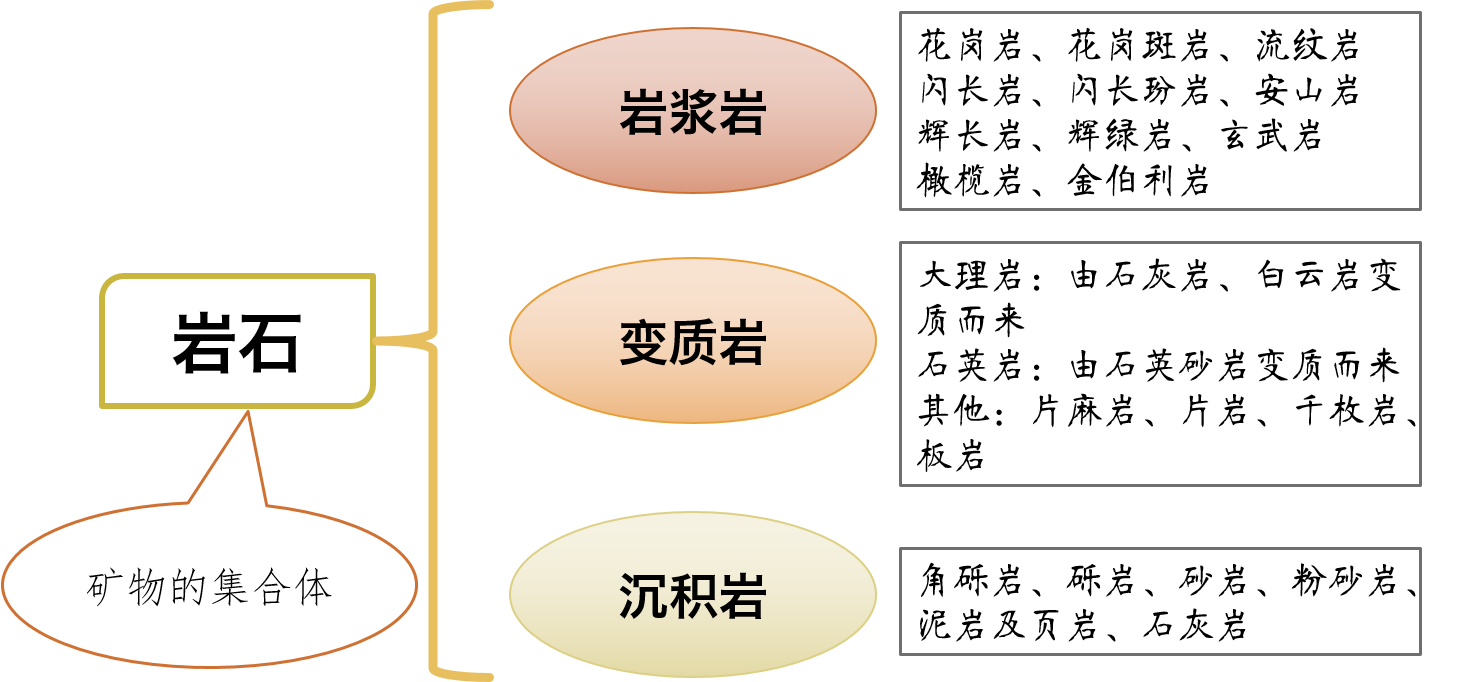
岩石是组成地壳的基本物质,它由各种造岩矿物或岩屑在地质作用下按一定规律组合而成。
矿物是指在地质作用下天然形成的结晶状纯净物(单质或化合物),是组成岩石的基础。像石英、长石、方解石都是常见的造岩矿物,但矿物和岩石不同,矿物可以用其化学式表示,而岩石是由许多矿物及非矿物所合成,没有一定的化学式。由一种矿物组成的岩石称作单矿岩,如大理岩由方解石或白云石组成,石英岩由石英组成等;由数种矿物组成的岩石称作复矿岩,如花岗岩由石英、长石和云母等矿物组成,辉长岩由基性斜长石和辉石组成。





























第一节 岩石的基本物理性质
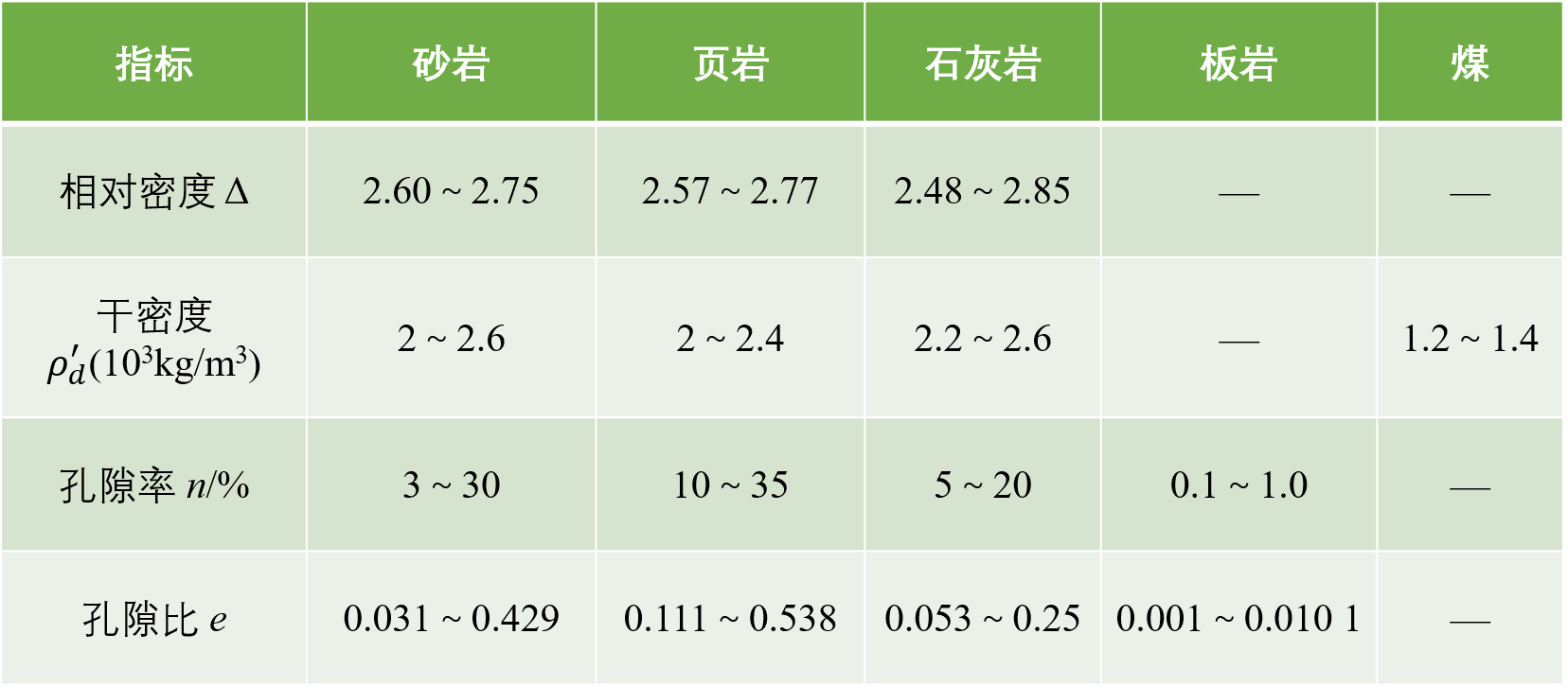
二、岩石的质量指标
- 天然密度:岩石在天然含水状态下的密度;
- 饱和密度(\( { \rho }_{ s }^{ ' } \)):岩石在吸水饱和状态下的密度;
- 干密度(\( { \rho }_{ d }^{ ' } \)):岩石在105~110℃下干燥24h后的密度;
- 体积力(\( \gamma \)):单位体积(包括孔隙体积)内岩石的质量所受的重力,又称岩石的容重;
- 相对密度(\( \Delta \)):岩石固体部分实体积(不包括孔隙体积)的重量与相同体积的4℃水的重量之比。
三、岩石的体积指标
岩石的孔隙性是岩石中孔洞和裂隙发育度的指标,常用孔隙度(也称孔隙率)表示,有时也用孔隙比表示。


三、岩石的体积指标
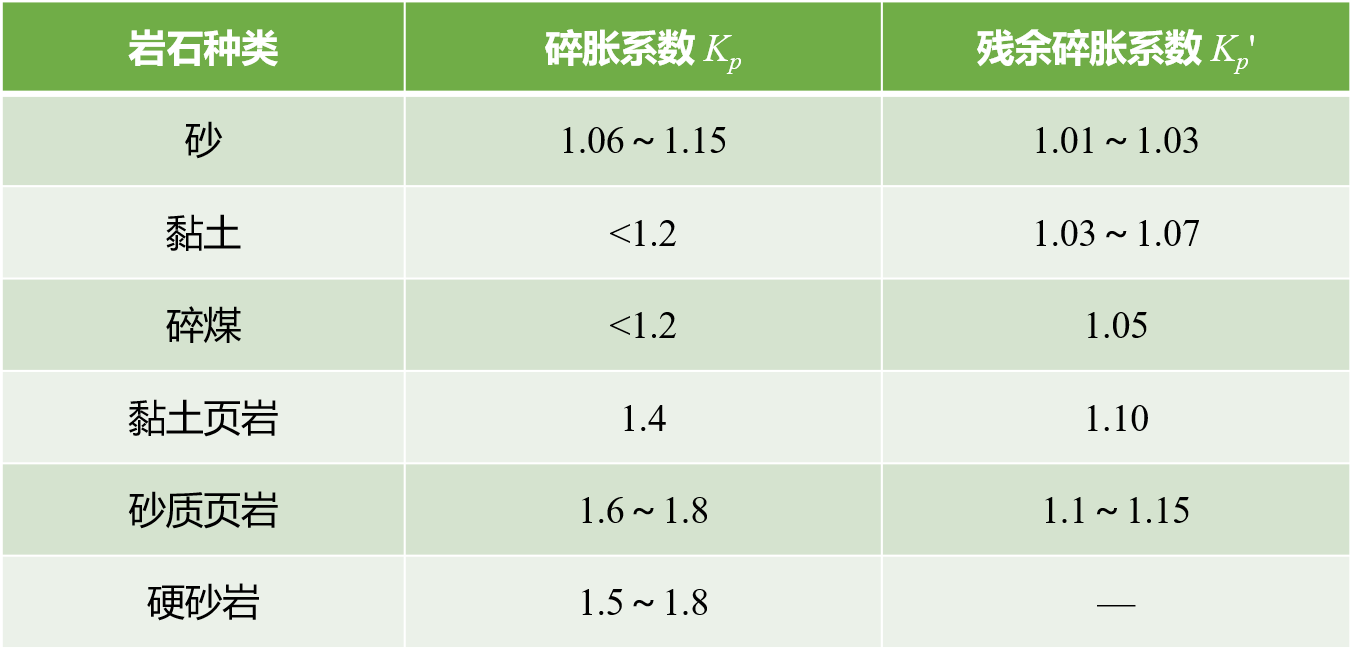
岩石的碎胀性是岩石破碎后的体积比破碎前的体积增大的性质。

岩石的压实性是岩石破碎后,在其自重和外加载荷作用下逐渐压实使体积减小的性质。
四、岩石的水理性质
1. 岩石的透水性
岩石能被水透过的性能称为岩石的透水性。当水在岩石中的流速较低时,其流动状态为层流,这时流速与压力梯度成正比(达西定律),即
\[v = - \frac{K}{\mu } \cdot \frac{{\partial p}}{{\partial x}}\]
式中,v 为水在岩石中的流速,K 为岩石的渗透率,μ 为水的动力粘性系数(又称绝对粘度),∂p/∂x 则为在x轴方向的水压力梯度。
四、岩石的水理性质
2. 岩石的软化性
岩石的软化性是指岩石浸水后其强度降低的性质,通常用软化系数 η0 表示水对岩石强度的影响程度。

四、岩石的水理性质
3. 岩石的膨胀性和崩解性
岩石的膨胀性和崩解性主要是松软岩石所表现出来的特征,尤其是含有大量黏土矿物(如蒙脱石、高岭土和水云母等)的软岩。
岩石的膨胀性是指软岩浸水后体积增大的性质,相应地会引起压力的增大。岩石遇水膨胀的特性可用膨胀应力和膨胀率两个指标表示。
岩石的崩解性是指软岩浸水后发生的崩解现象。
四、岩石的水理性质
4. 岩石的吸水性和抗冻性
遇水不崩解的岩石在一定实验条件下(规定的试样尺寸和实验压力)吸入水分的性能称为岩石的吸水性。通常以岩石的自然吸水率、饱和吸水率和饱水系数表示。
岩石的抗冻性是指岩石抵抗冻融破坏的能力。
五、岩石的热性和电磁性
1. 岩石的容热性和热膨胀性
岩石的容热性指岩石进行热交换时所吸收热量的能力,用岩石的比热容(c)和比定容热容(cv)表示。
- 比热容指不存在相转变条件下,单位质量的岩石温度变化1℃(或1K)时所需热量,单位是J/(kg·℃)或J/(kg·K);
- 比定容热容指使单位体积的岩石温度变化1℃(或1K)时所需热量,单位是J/(m3·℃)或J/(m3·K)。
岩石的比热容取决于岩石中所含矿物的成分及含量,但温度和压力变化范围不大时,岩石的比热容可视为常数。
五、岩石的热性和电磁性
1. 岩石的容热性和热膨胀性
岩石的热膨胀性指岩石受热后长度和体积发生膨胀的性质,常用线膨胀系数(al)和体膨胀系数(av)表征。
- 线膨胀系数指岩石试件在温度每升高1℃(或1K)时所引起的长度增量与其0℃(或273.15K)时长度之比;
- 体膨胀系数是岩石试件在温度每升高1℃(或1K)时所引起的体积增量与其0℃(或273.15K)时体积之比。
岩石的线膨胀系数因岩石中所含矿物成分的不同而不同。
五、岩石的热性和电磁性
2. 岩石的电磁特性
任何岩石都具有电磁特性,在工程地质勘探过程及矿山异常动力现象研究中,有时要用到岩石的电磁特性,其表征指标有岩石的导电性和磁性。
岩石的导电性是指岩石介质传导电流的能量,常用电阻率表示。岩石的电阻率是指沿岩石试样体积电流方向的直流电场强度与该处电流密度的比值。
岩石的磁性包括感应磁性及剩余磁性。前者指岩石被现代地磁场磁化而产生的磁性;后者指岩石形成过程中被当时地磁场磁化所保留下来的磁性。
第二节 岩石的强度和变形特性
第二节 岩石的强度和变形特性
一、岩石的变形特性
岩石的变形性质是指岩石在不同类型受载下发生形状和体积的变化的性质。
1. 岩石变形性质的类别

一、岩石的变形特性
岩石的弹性变形是指卸载后岩石变形能完全恢复到其原始状态的性质。它包括:
- 线弹性:应力应变关系呈直线关系;
- 完全弹性(非线性弹性):应力应变关系不是直线关系,但卸载时应力应变沿原来的曲线返回原点;
- 滞弹性:应力应变关系为曲线关系,无残余变形,卸载时应力应变沿另一条曲线返回原点。
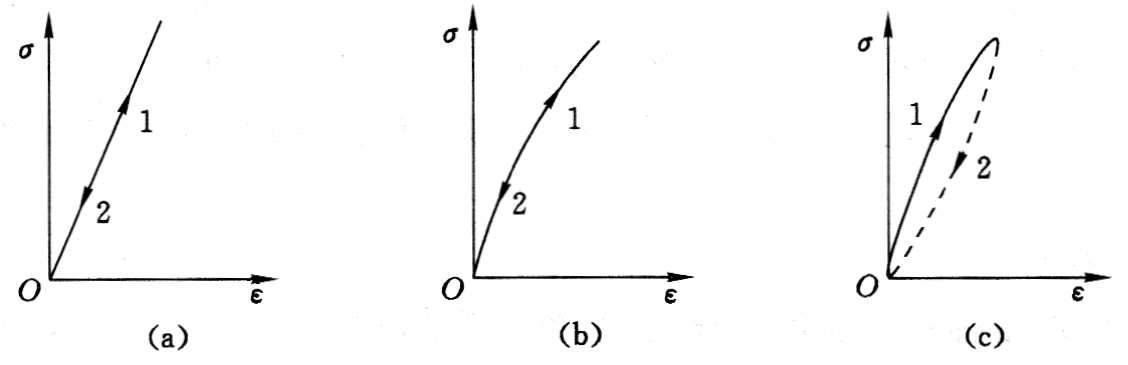
(a)线弹性;(b)非线性弹性;(c)滞弹性
1—加载过程;2—卸载过程
一、岩石的变形特性
岩石的塑性变形是指岩石在外力作用下当超过其屈服极限应力时仍能发生变形,撤去外力后不能完全恢复其原始状态的性质,亦称残余变形。它包括:
- 理想塑性:当应力低于屈服极限(屈服应力)σy时,岩石的性质为弹性;当应力超过屈服应力后,应力不变而变形不断增长,应力应变曲线为水平线,此时岩石所能承受的最大载荷为其屈服应力。
- 应变硬化:当应力低于屈服极限(屈服应力)σy时,岩石的性质为弹性;当应力超过屈服应力后,出现塑性变形,但应力和变形都不断增加,应力应变曲线呈上升变化,随着变形的发展,岩石的承载力也会增长。
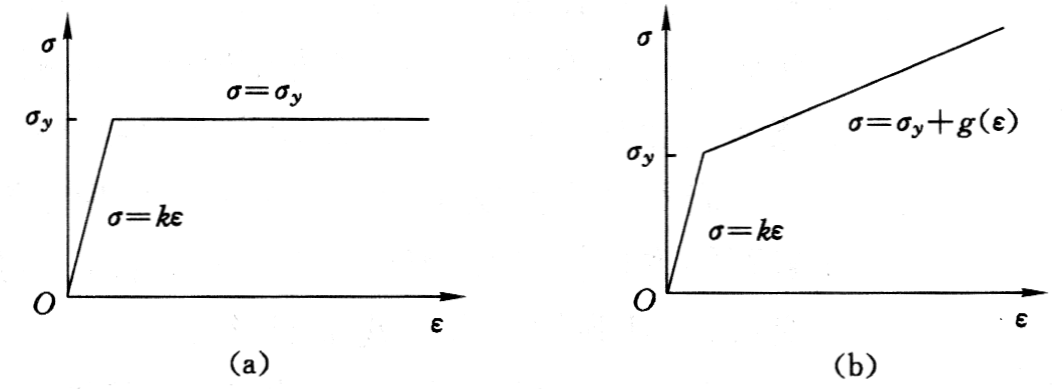
(a)理想弹塑性;(b)线性强化弹塑性(应变硬化)
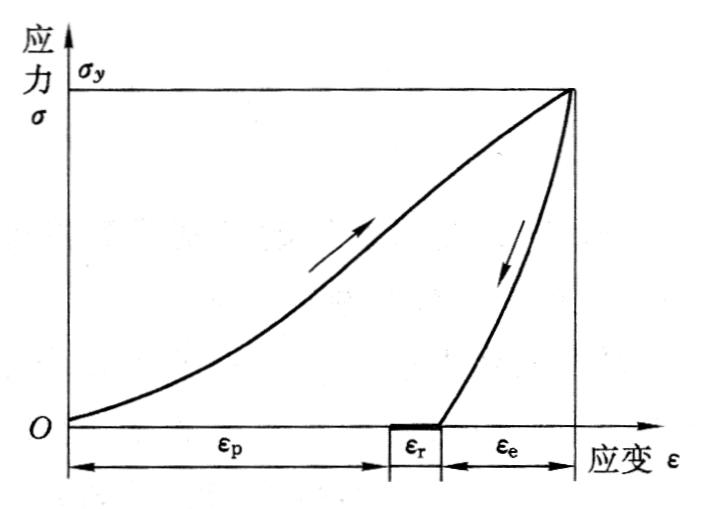
\( { \varepsilon }_{ e } \)—瞬时弹性变形;\( { \varepsilon }_{ r } \)—弹性后效变形;\( { \varepsilon }_{ p } \)—永久塑性变形
一般岩石的变形特性:
- 岩石的变形特性与其类型、物理性质、加载方式、载荷大小及作用时间等有关,且岩石的弹性和塑性变形往往同时出现。
- 在一般加载条件下,岩石只在较小的应力范围内可看作是弹性介质,即其应力应变关系可看作服从胡克(Hook)定律,但多数不遵从。
- 岩石的变形包括瞬时弹性变形、后效弹性变形和塑性变形三个部分。
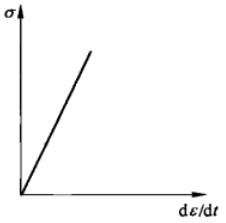
岩石的黏性是指岩石在外力作用下变形不能在瞬间完成,且应变的速率随应力的变化而改变,当外力撤去后,不能恢复其原始状态的性质。
理想的黏性岩石材料,其应力与应变速率曲线呈直线关系,并且通过原点。这种应变速率随应力而改变的变形称之为流变变形或流动变形。
一、岩石的变形特性
2. 单轴压缩条件下岩石的变形特性
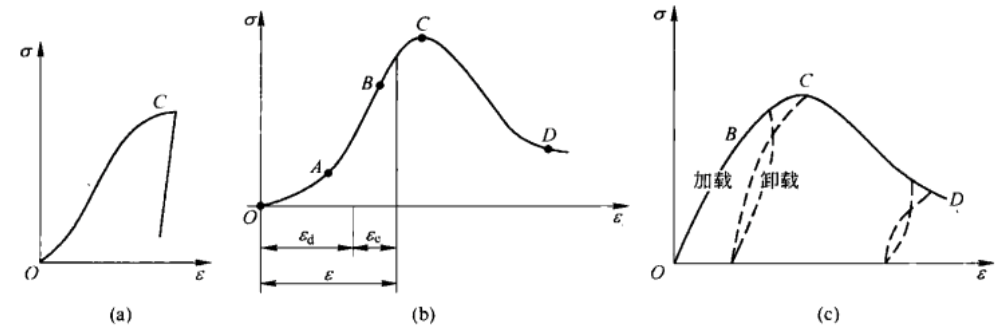
(a)普通试验机;(b)刚性试验机;(c)刚性试验机反复加卸载
一、岩石的变形特性
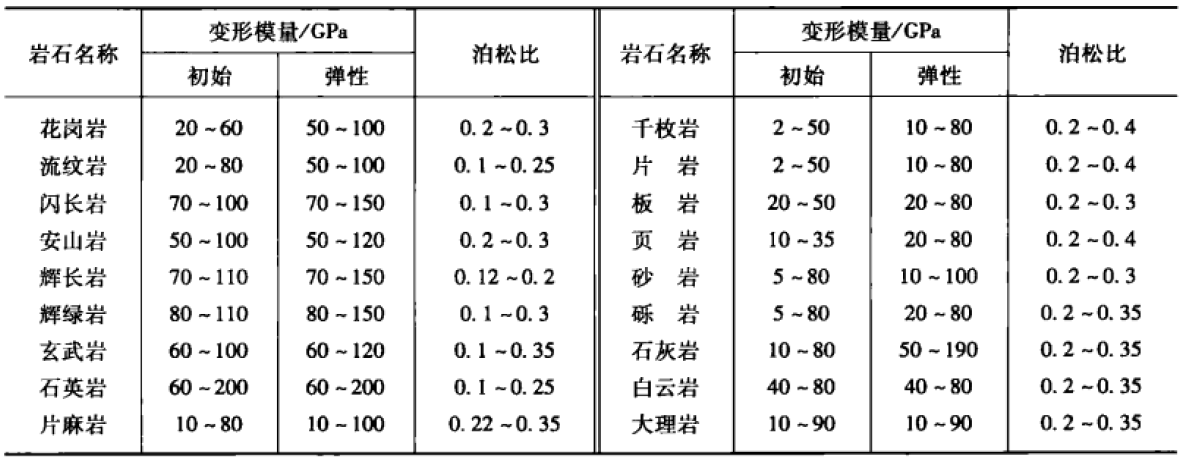
3. 岩石变形指标
\[\mu = - \frac{{{\varepsilon _c}}}{{{\varepsilon _a}}}\]
μ—岩石的泊松比;εc,εa—岩石试件的横向应变、轴向应变。
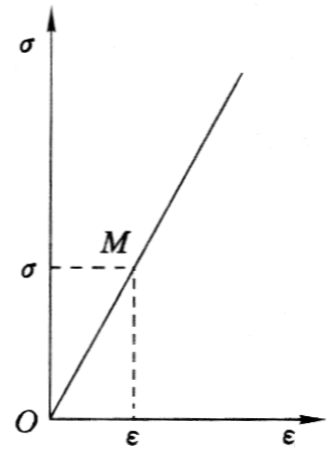
3. 岩石变形指标
(1)线弹性变形,弹性模量E为应力除以应变,即应力应变曲线的直线斜率。
\[E = \frac{\sigma }{\varepsilon }\]
(2)非线性变形:
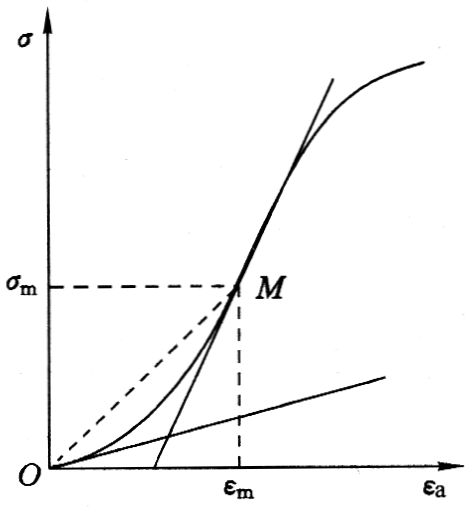
① 初始模量
\[E = {\left. {\frac{{{\rm{d}}\sigma }}{{{\rm{d}}\varepsilon }}} \right|_{\varepsilon = 0}}\]
② 切线模量
\[E = {\left. {\frac{{{\rm{d}}\sigma }}{{{\rm{d}}\varepsilon }}} \right|_{\varepsilon = {\varepsilon _m}}}\]
③ 割线模量
\[E = \frac{{{\sigma _m}}}{{{\varepsilon _m}}}\]
3. 岩石变形指标
\[{E_t} = \frac{\sigma }{{{\varepsilon _e} + {\varepsilon _r} + {\varepsilon _p}}}\]
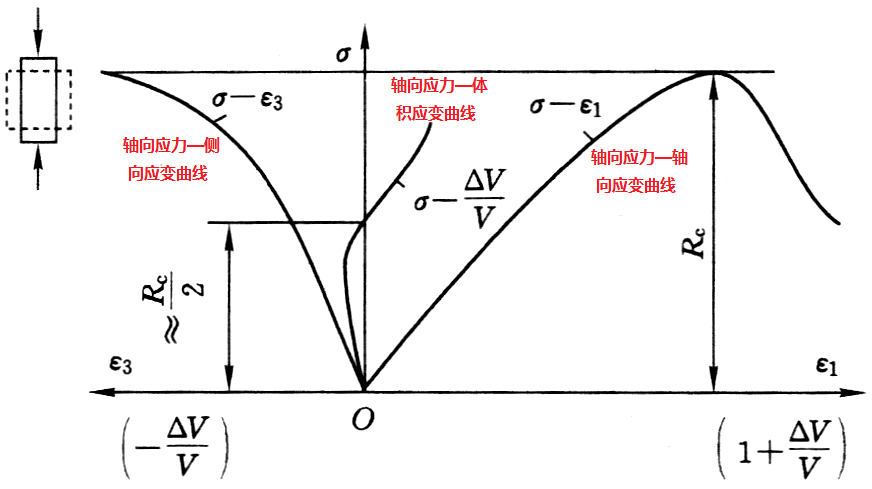
试件的体积变化
岩石试件在单轴受压试验中,始终伴随着体积变化,其特点是:弹性阶段,体积减小;塑性阶段,体积膨胀,且试件要先恢复到原体积而后超过原体积。
岩石在塑性阶段的体积膨胀称为扩容现象,该现象主要是由于裂隙产生、贯穿、张开等造成的,相对于原体积来说,体积由减小到增大大约在\(\sigma = {\sigma _c}/2\)附近。
通常用体积应变\({\varepsilon _V}\)来表征体积的变化,即
\[{\varepsilon _V} = \frac{{\Delta V}}{V} = {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3} = \frac{{1 + 2\mu }}{E}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)\]
当岩石为各向同性的弹性材料时,其体积变形特征还可用体积变形模量K(简称体积模量)来表示,即岩石处于静水应力状态时单位体积的体积变化所需要的静水压力,也称为容变弹性模量。
\[{K} = \frac{E}{{3\left( {1 - 2\mu } \right)}}\]
第二节 岩石的强度和变形特性
二、岩石的强度特性
岩石的强度:岩石在各种载荷作用下达到破坏时所能承受的最大应力。根据载荷作用形式的不同,通常有:
- 单轴抗压强度(非限制性抗压强度)
- 单轴抗拉强度
- 抗剪强度
- 三轴抗压强度
- 更多……
二、岩石的强度特性
1. 岩石的单轴抗压强度
岩石在单轴压缩载荷作用下达到破坏前所能承受的最大压应力称为岩石的单轴抗压强度(uniaxial compressive strength),或称为非限制性抗压强度(unconfined compressive strength)。国际上通常把单轴抗压强度表示为UCS,我国习惯于将单轴抗压强度表示为\( { \sigma }_{ c } \),其值等于达到破坏时的最大轴向压力P除以试件的横截面积A,即
\[{\sigma _c} = \frac{P}{A}\]
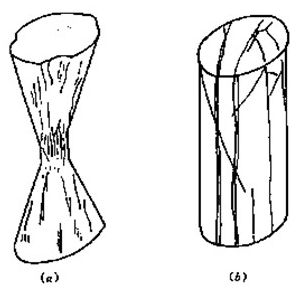
(a)圆锥形破坏;
(b)柱状劈裂破坏
测定方法:
制作一定规格的试件(通常为圆柱体),放在带有上、下块承压板的材料试验机内,按每秒0.5~1.0MPa的速度加压直至试件破坏,记录破坏载荷以及加压过程中出现的现象,并对破坏后的试件进行描述或摄影,计算单轴抗压强度。

- OA:原始孔隙压密阶段;
- AB:弹性变形阶段;
- BC:塑性强化阶段(弹塑性过渡阶段);
- CD:残余承载阶段(破坏阶段,后破坏阶段);
- B点为屈服点,该点的应力称为屈服应力;
- 岩石从C点开始破坏,该点应力称为峰值强度、强度极限,常用\( { \sigma }_{ max } \)、\( { R }_{ c } \)或\( { \sigma }_{ c } \)表示
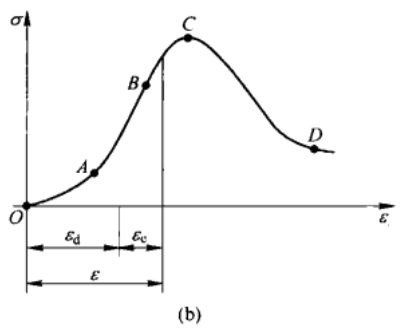
全应力—应变曲线
二、岩石的强度特性
2. 岩石的单轴抗拉强度
岩石试件在受到轴向拉应力后发生破坏时的单位面积所能承受的拉力。
测定方法:
- 直接拉伸法
- 抗弯法
- 劈裂法
- 点载荷试验法
直接拉伸法
将岩石加工成棒状,并利用岩石试件的两端与试验机夹具之间的粘结力或摩擦力,对岩石试件直接施加拉力。
\[{\sigma _t} = \frac{P_t}{A}\]
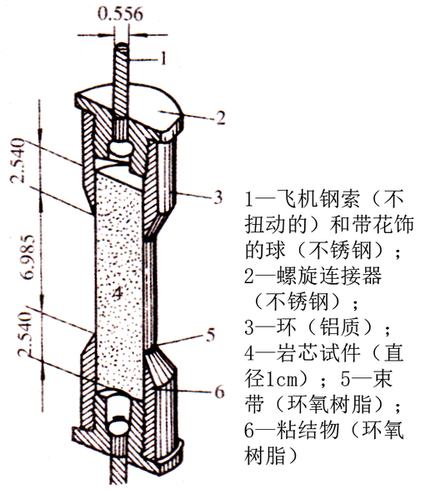
抗弯法
利用结构试验中梁的三点或四点加载的方法,使梁的下沿产生纯拉应力的作用而使岩石试件产生拉断裂破坏,间接地求出岩石的抗拉强度的一种试验方法。此时,其抗拉强度值可按下式求得:
\[{\sigma _t} = \frac{{MC}}{I}\]
式中:M—作用在试件截面上的最大弯矩;C—梁的边缘到中性轴的距离;I—梁截面绕中性轴的惯性矩。
劈裂法
劈裂法也称作径向压裂法,因为南美巴西人杭德罗斯(Hondros)提出的试验方法,故也称巴西法。其方法是:用一个实心圆柱形试件,使它承受径向压缩线载荷至破坏,间接地求出岩石的抗拉强度。由于该方法试件加工方便,试验简单,是目前最常用的抗拉强度试验方法。
\[{\sigma _t} = \frac{{2P}}{{Dt\pi }}\]
式中:P—试件破坏时的极限压力;D—试件的直径;t—试件的厚度。
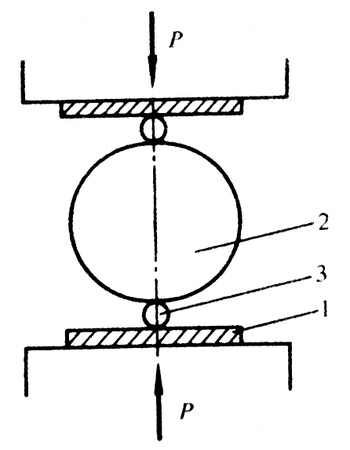
1—承压板;2—试件;3—钢丝
点载荷试验法
一种简便的现场试验方法,可利用现场取得的任何形状的岩块,其实验装置是一个极为小巧的设备。其原理类似于劈裂法,不同的是劈裂法所施加的是线载荷,而本方法所施加的是点载荷。
\[{\sigma _t} = 0.96{I_s} = 0.96\frac{P}{{D_e^2}}\]
式中:Is—点载荷强度指数;P—试验时所施加的极限载荷;De—试验时两个加载点之间的距离
二、岩石的强度特性
3. 岩石的抗剪强度
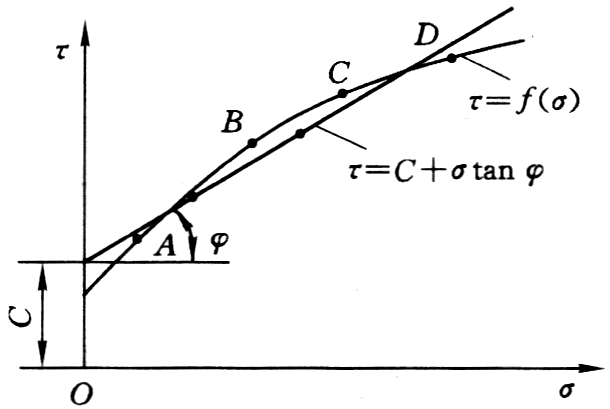
岩石在一定的应力条件下(主要指压应力)所能抵抗的最大剪应力。通常用\(\tau \)表示。该强度是在复杂应力作用下的强度,与岩石的抗压、抗拉强度不同,需要用一组岩石的试验结果来描述岩石的抗剪强度。因此岩石的抗剪强度通常用以下的函数式表示:
\[\tau = f\left( \sigma \right)\]
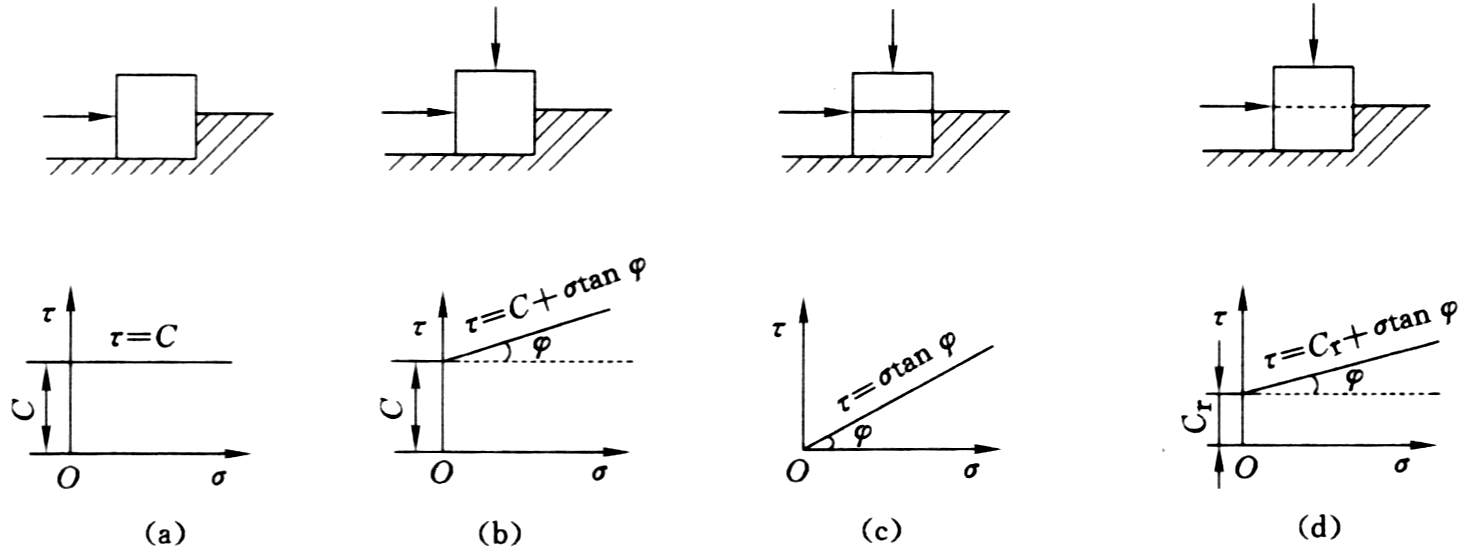
(a)抗切实验;(b)抗剪实验;(c)摩擦实验;(d)重剪实验
3. 岩石的抗剪强度
根据岩石剪切试验的结果,常用莫尔—库伦公式表示岩石的强度:
\[\tau = \sigma \tan \varphi + c\]
式中:σ—作用破坏面上的正应力;φ—岩石的内摩擦角;c—岩石的内聚力。
岩石的抗剪强度的测定方法
- 非限制性剪切强度试验
- 单面剪切试验
- 双面剪切试验
- 冲击剪切试验
- 扭转剪切试验
- 限制性剪切强度试验
- 抗切实验(直剪试验)
- c、φ值的简便求解法
- 角模压剪试验
- 残余剪切强度
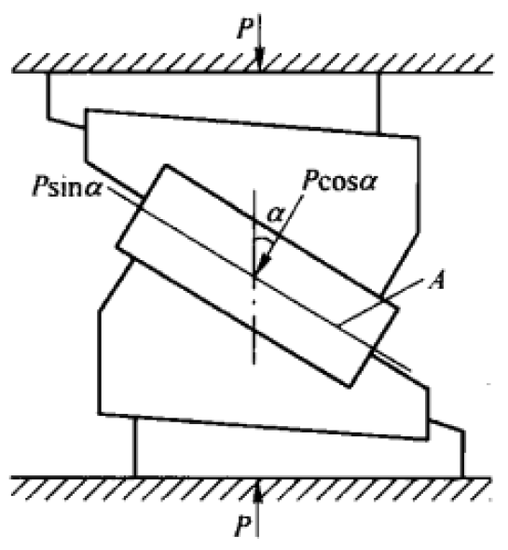
试件受力示意图
二、岩石的强度特性
4. 岩石的三轴抗压强度
在不同的三向压缩应力作用下岩石抵抗外载荷的最大应力。表示为:
\[\tau = f\left( {{\sigma _1},{\sigma _2},{\sigma _3}} \right)\]
该强度在三轴压力试验机上测定。测定时先设定侧向应力σ2和σ3,再逐渐增加轴向应力σ1直至试件破坏。
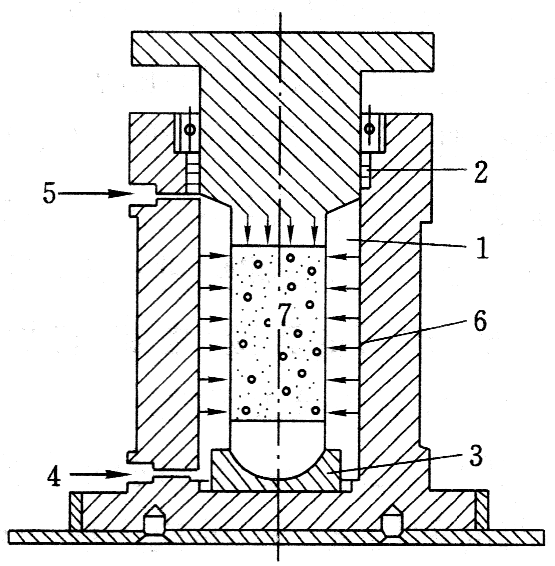
1—压力室;2—密封设备;3—球面底座;4—压力液;5—排气口;6—侧压力;7—试样
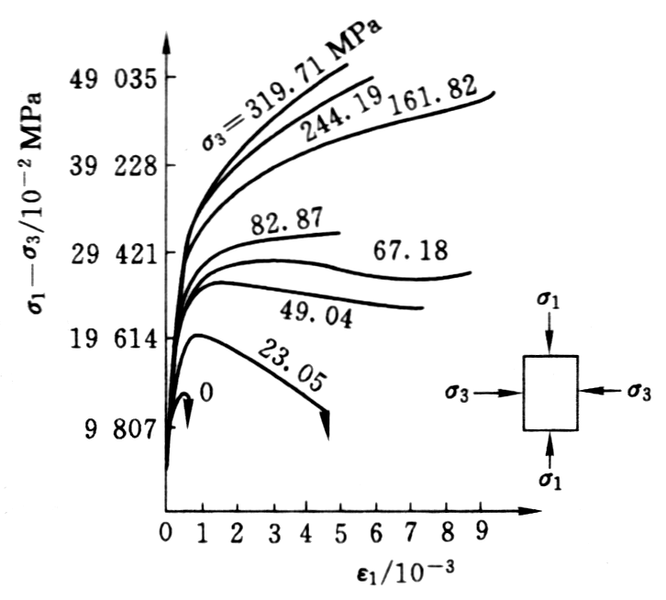
4. 岩石的三轴抗压强度
围压对岩石变形的影响规律。随着围压的增大:
- 岩石的抗压强度显著增加;
- 岩石的变形显著增大,产生明显塑性变形;
- 岩石的弹性极限显著增大;
- 岩石的应力—应变曲线形态发生明显改变,岩石的性质发生了变化:由弹脆性→弹塑性→应变硬化;
- 不同岩石弹性模量变化规律不同。
二、岩石的强度特性(总结)
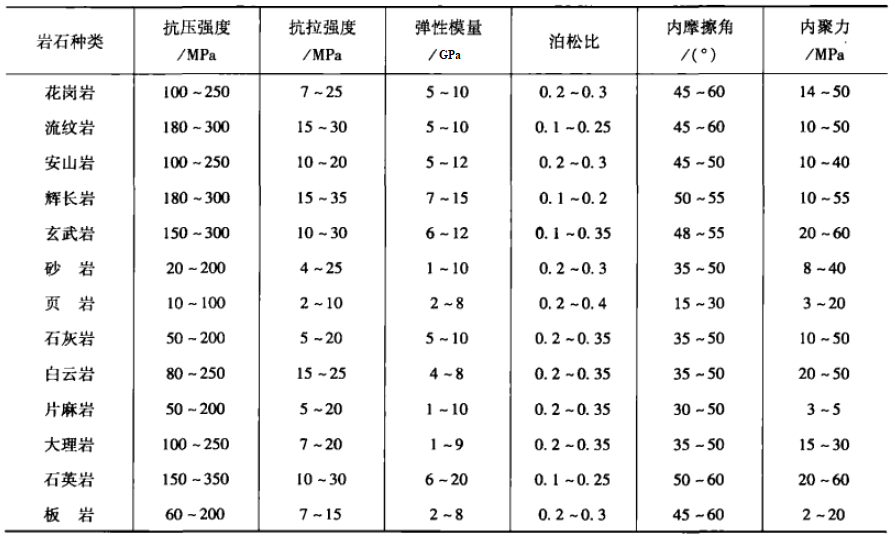
总之,岩石强度因受力状态变化而异,其强度相差甚远。岩石强度的大小关系为:三轴等压抗压 > 三轴不等压抗压 > 双向抗压 > 单轴抗压 > 抗剪 > 抗弯 > 抗拉。岩石的单轴抗拉强度一般为单轴抗压强度的1/10左右。
因此,在工程中要尽量使岩体处于有利的受力状态,充分发挥岩体的强度,力求避免岩体处于受拉状态。
三、岩石的流变特性
岩石的变形不仅表现出弹性和塑性,而且还具有流变性。岩石的应力应变关系随时间变化而变化的性质,称为岩石的流变性质。岩石的流变性质包括:
- 蠕变:指当应力不变时,应变随时间增长而增大的现象。
- 松弛:指当应变不变时,应力随时间延长而减小的现象。
- 弹性后效:加载或卸载时,弹性应变滞后于应力的现象。
三、岩石的流变特性
1. 岩石的蠕变特性
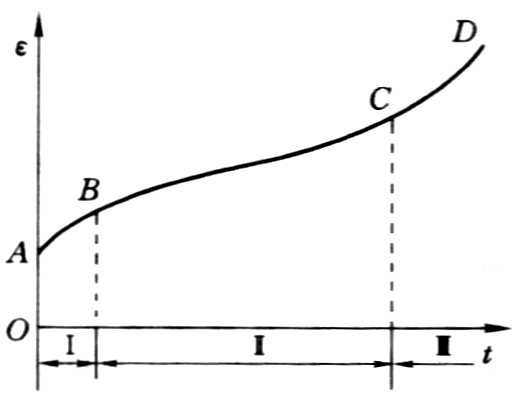
(1)OA段:瞬时变形阶段。
(2)AB段:第一阶段蠕变(又称初始蠕变、过渡蠕变或阻尼蠕变)。此段应变不断增加,但增长速率却随时间降低,曲线呈下凹形。
(3)BC段:第二阶段蠕变(又称等速蠕变或定常蠕变)。此段时间延续最长,应变随时间呈近似的等速增长。
(4)CD段:第三阶段蠕变(又称加速蠕变)。当应变到达C点后加速增长,曲线呈上凹形,当应变达到某个数值D点时试件被破坏。
三、岩石的流变特性
1. 岩石的蠕变特性
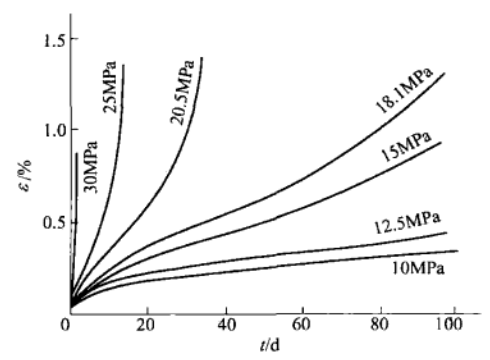
不同应力条件下岩石的蠕变曲线并不相同,如右图:
(1)稳定蠕变。图中σ≤12.5MPa时的两条曲线。蠕变变形的速率随时间增长而减小,最后趋于稳定。稳定蠕变一般不会导致岩体整体失稳。
(2)非稳定蠕变。又可分为:
- 典型的蠕变。图中σ=15MPa和σ=18.1MPa的两条曲线(其解释见前一页)。
- 加速蠕变:如图中σ≥20.5MPa的三条曲线。曲线几乎无稳定蠕变阶段。
三、岩石的流变特性
1. 岩石的蠕变特性
三、岩石的流变特性
2. 岩石的流变模型
流变的物理力学过程十分复杂,通常应用基本元件建立流变模型。所有的流变模型均可由三个基本元件组合而成:
- 弹性元件(胡克体,以符号H代表)。该体的力学模型用一个弹簧元件表示。其应力—应变关系为线弹性的。
- 黏性元件(牛顿体,以符号N代表)。该体的力学模型用一个带活塞组成的阻尼器表示。该体为理想黏性体,符合牛顿流动定义,即应力与应变速率成正比。
- 塑性元件(库伦体,以符号C代表)。该体的力学模型用一个摩擦片(或滑块)表示。该体为理想塑性体,即物体所受的应力达到屈服极限时便开始产生塑性变形,即使应力不再增加,变形仍不断增加。
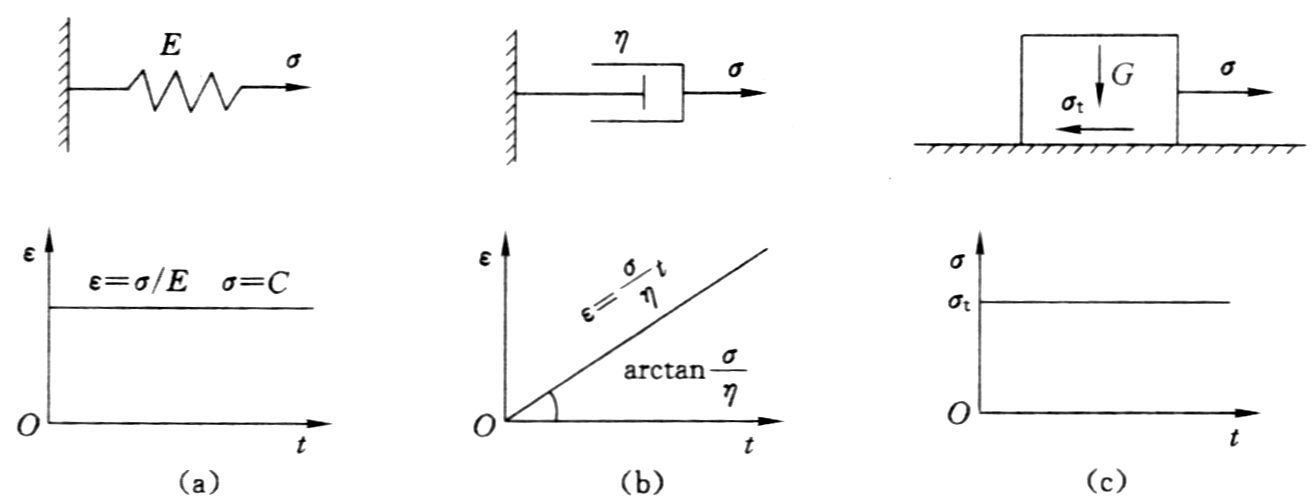
(a)弹性体;(b)黏性体;(c)塑性体
三、岩石的流变特性
2. 岩石的流变模型
组合模型:客观存在的岩石性质表现为以上三种元件的组合。组合的方式为串联、并联、串并联和并串联。并联和串联的性质:
- 串联
- 应力:组合体总应力等于串联中任何元件的应力(σ=σ1=σ2);
- 应变:组合体总应变等于串联中所有元件的应变之和(ε=ε1+ε2)。
- 并联
- 应力:组合体总应力等于并联中所有元件的应力之和(σ=σ1+σ2);
- 应变:组合体总应变等于并联中任何元件的应变(ε=ε1=ε2)。
三、岩石的流变特性
2. 岩石的流变模型
已经提出了几十种流变体的组合模型,他们大多数是利用提出者的名字命名的。如麦克斯韦体(Maxwell)、开尔文体(Kelvin)、广义开尔文体(General Kelvin)、鲍埃丁—汤姆逊体(Poyting-Thomson)、理想黏塑性体、伯格斯体(Burgers)、西原体、宾汉姆林体(Bingham)等。
四、影响岩石变形和强度的因素
- 岩石的性质
- 岩石的生成条件
- 岩石的构造特征
- 风化、水和温度的作用
- 岩石试件的形状和尺寸
- 加载速率及次数
- 岩石的受载状态
五、煤和岩石物理力学性质测定方法
GB/T23561《煤和岩石物理力学性质测定方法》,分为16个部分:
- 第1部分:采样一般规定;
- 第2部分:煤和岩石真密度测定方法;
- 第3部分:煤和岩石块体密度测定方法;
- 第4部分:煤和岩石孔隙率计算方法;
- 第5部分:煤和岩石吸水性测定方法;
- 第6部分:煤和岩石含水率测定方法;
- 第7部分:单轴抗压强度测定及软化系数计算方法;
- 第8部分:煤和岩石变形参数测定方法;
五、煤和岩石物理力学性质测定方法
GB/T23561《煤和岩石物理力学性质测定方法》,分为16个部分:
- 第9部分:煤和岩石三轴强度及变形参数测定方法;
- 第10部分:煤和岩石抗拉强度测定方法;
- 第11部分:煤和岩石抗剪强度测定方法;
- 第12部分:煤的坚固性系数测定方法;
- 第13部分:煤和岩石点载荷强度指数测定方法;
- 第14部分:岩石膨胀率测定方法;
- 第15部分:岩石膨胀应力测定方法;
- 第16部分:岩石耐崩解性指数测定方法。
第三节 岩石的破坏机理和强度理论
一、岩石的破坏机理
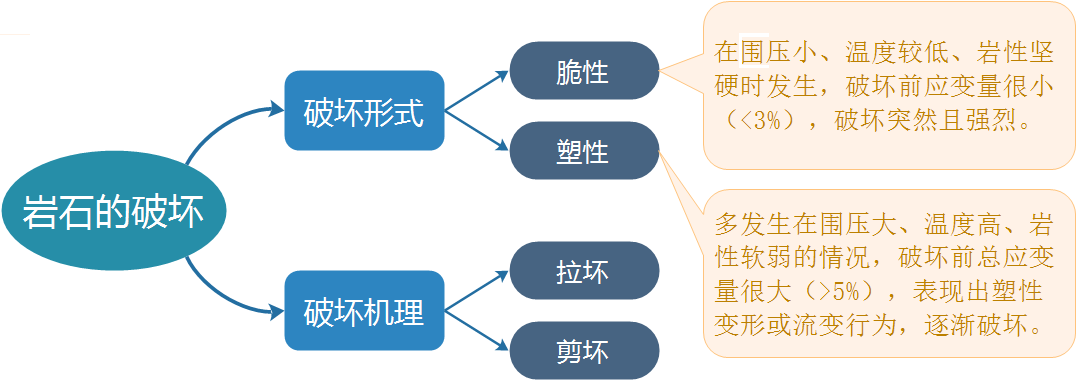
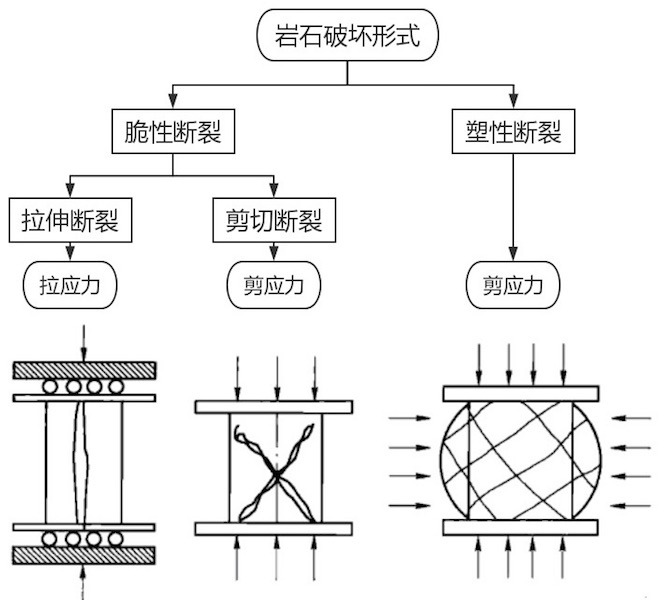
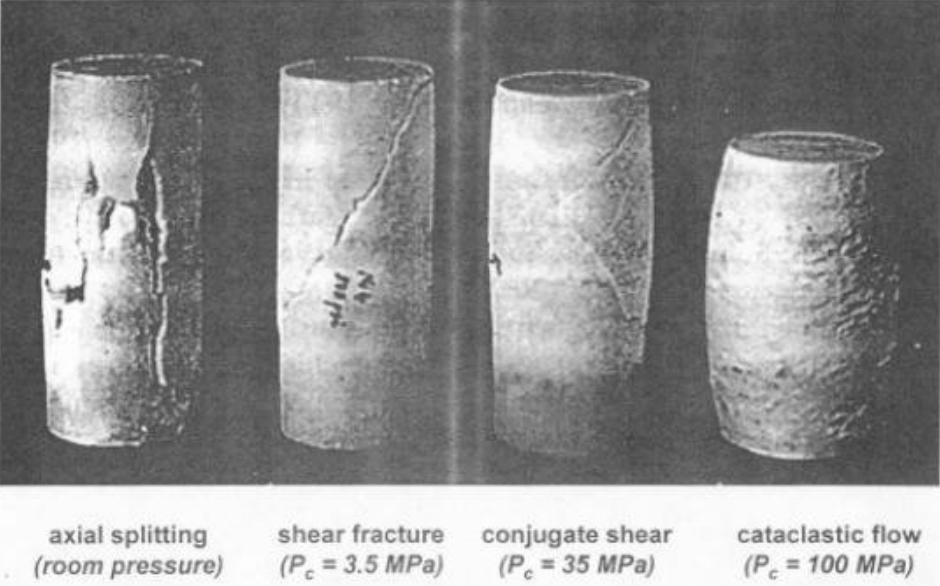
第三节 岩石的破坏机理和强度理论
二、莫尔强度理论
莫尔(Mohr)于1900年提出了莫尔强度理论,认为材料发生破坏是由于材料在某一面上剪应力达到一定的限度(即极限剪应力),而这个剪应力与材料本身性质和正应力在破坏面上所造成的摩擦阻力有关。即材料发生破坏除了取决于该点的剪应力,还与该点正应力相关。
这是目前岩石(体)力学中应用最为广泛的理论。
二、莫尔强度理论
1. 莫尔应力圆(表示材料上一点的应力状态)
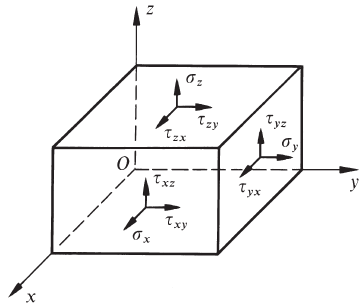
应力张量:
\[\sigma_{ij} = \begin{bmatrix} \sigma_{x} & \tau _{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_{y} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{z} \end{bmatrix}\]
二、莫尔强度理论
1. 莫尔应力圆(表示材料上一点的应力状态)
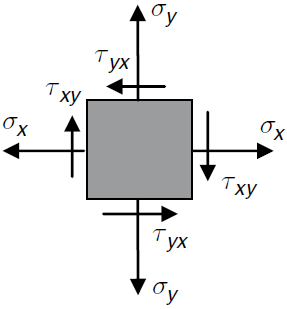
应力张量:
\[\sigma_{ij} = \begin{bmatrix} \sigma_{x} & \tau _{xy}\\ \tau_{yx} & \sigma_{y} \end{bmatrix}\]
在平面应力状态下,有两个主应力\(\left( {{\sigma _1},{\sigma _3}} \right)\)作用在某一点上,则最大主应力\({\sigma _1}\)与外法线成\({\alpha}\)角的斜切面上法向应力\({\sigma _\alpha}\)和剪应力\({\tau_\alpha}\)的表达式为:
\[\left. \begin{array}{l} {\sigma _\alpha } = \frac{{{\sigma _1} + {\sigma _3}}}{2} + \frac{{{\sigma _1} - {\sigma _3}}}{2}\cos 2\alpha \\ {\tau _\alpha } = \frac{{{\sigma _1} - {\sigma _3}}}{2}\sin 2\alpha \end{array} \right\}\]
说明在\(\sigma - \tau \)平面内,一点的应力状态可用一个圆来表示:
\[{\left( {{\sigma _\alpha } - \frac{{{\sigma _1} + {\sigma _3}}}{2}} \right)^2} + \tau _\alpha ^2 = {\left( {\frac{{{\sigma _1} - {\sigma _3}}}{2}} \right)^2}\]
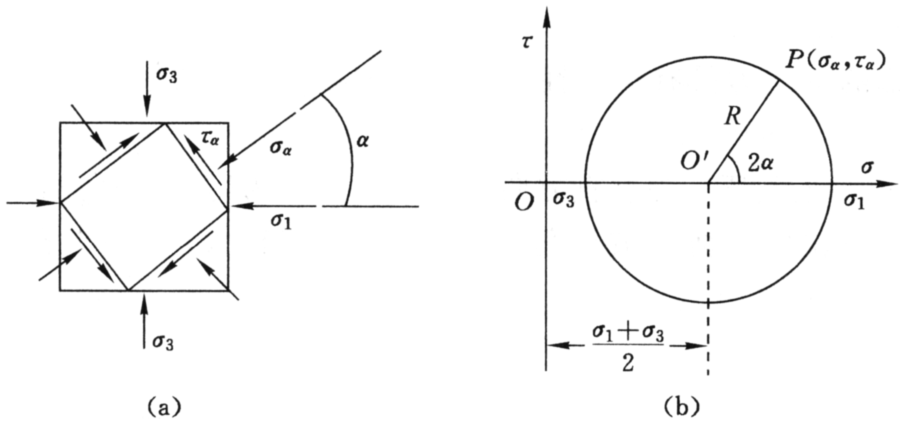
二、莫尔强度理论
2. 强度曲线
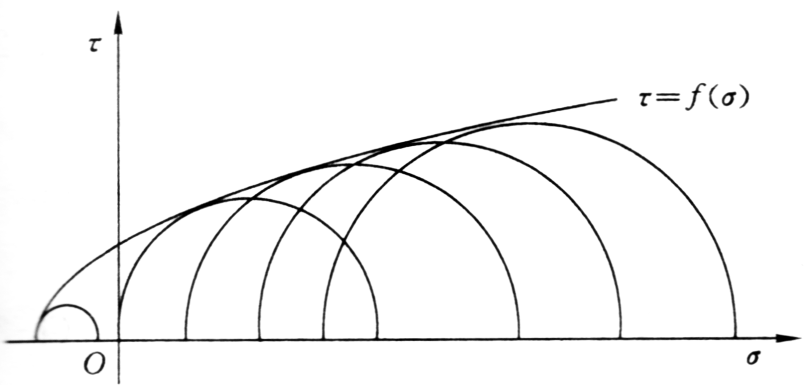
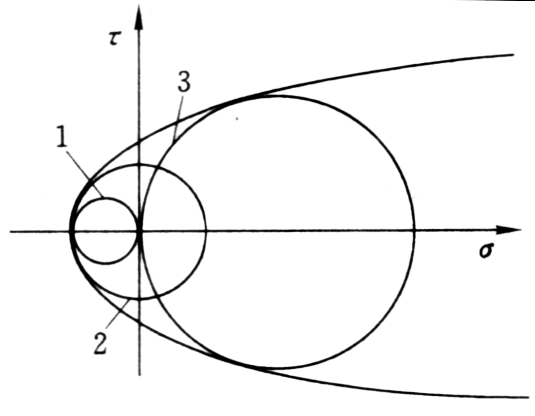
1—单拉;2—纯剪;3—单压
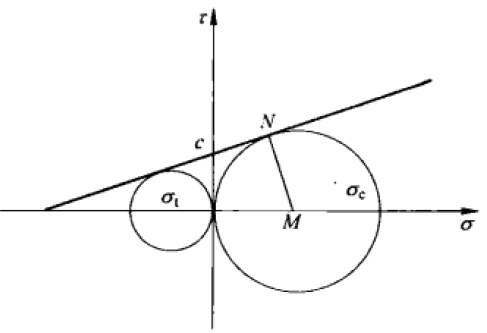
强度曲线的主要用途
- 反映岩石抵抗拉、压等破坏的能力;
- 预测破坏面的方向;
- 直接判断岩石是否破坏。
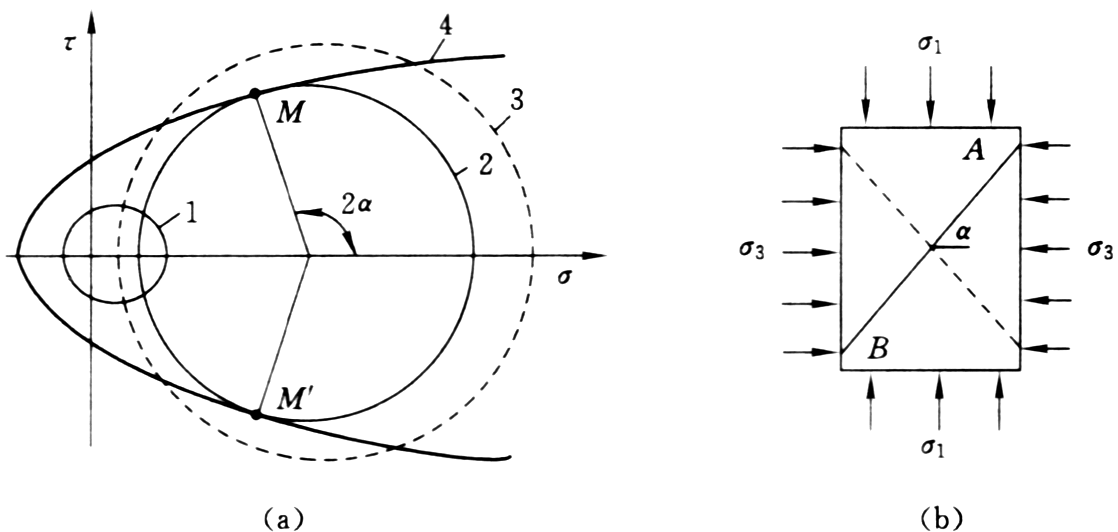
(a)极限应力图;(b)X形剪切破坏
二、莫尔强度理论
3. 莫尔强度准则
(1)莫尔—库伦强度准则
目前应用最为广泛的强度准则,先由库伦(Coulomb)在1773年提出,后来莫尔用新理论加以解释,故称作莫尔—库伦强度准则。
该准则认为当压力不大时(一般σ<10MPa),可用斜直线强度曲线推导出强度准则的表达式为(下页):
(1)莫尔—库伦强度准则
\[\tau = c + \sigma \tan \varphi \]
式中:
- c——岩石的粘聚力(内聚力);
- φ——岩石的内摩擦角。
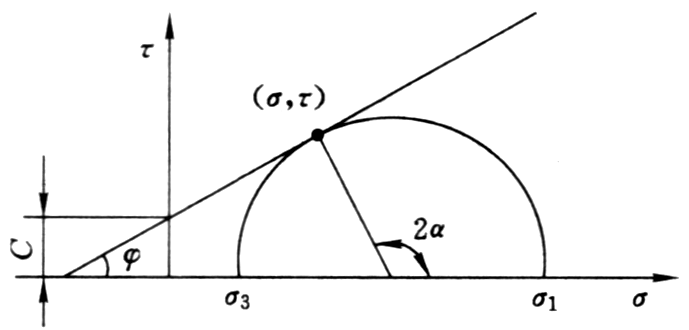
(1)莫尔—库伦强度准则
利用斜直线强度曲线可得出以下结论:
① 确定单轴抗压与抗拉强度的比为:
\[\frac{{{\sigma _c}}}{{{\sigma _t}}} = {\text{tan} ^2} \left( {45{\rm{^\circ + }}\frac{\varphi }{2}} \right)\]
利用斜直线强度曲线可得出以下结论:
② 确定剪切破坏面与最大主应力平面的夹角(即剪切破坏角):
\[\alpha = 45^\circ + \frac{\varphi }{2}\]
③ 确定三轴应力状态下的抗压强度值:
\[{\sigma _1} = {\sigma _c} + \frac{{1 + \sin \varphi }}{{1 - \sin \varphi }}{\sigma _3}\]
3. 莫尔强度准则
(2)双曲线形强度曲线(略)
(3)抛物线形强度曲线(略)
第三节 岩石的破坏机理和强度理论
三、格里菲斯强度理论
格里菲斯(A.A.Griffith)于1921年提出了关于脆性材料破裂的理论。他认为,在材料内部存在许多均匀、随机地分部的窄缝形的裂隙。在力的作用下,处于不利方位的裂隙端就产生应力集中现象,使该处的应力达到所施加压力的几十倍甚至上百倍,于是裂隙就沿其长度方向开始扩张,直至材料整体破坏。
三、格里菲斯强度理论
1. 裂纹扩展的能量准则
能量释放率G
=
表面能增加率R
\[\frac{{{\rm{d}}U}}{{{\rm{d}}b}} = \frac{{{\rm{ds}}}}{{{\rm{d}}b}}\]
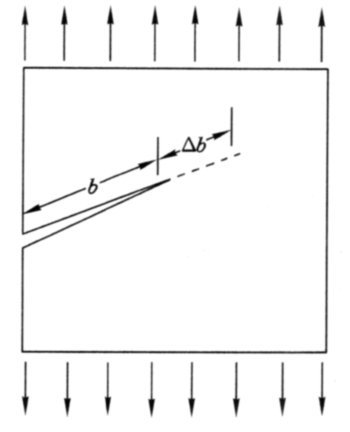
三、格里菲斯强度理论
2. 裂纹扩展的应力准则
靠近裂隙尖端处应力值达到该点材料的抗拉强度时,才会从这个裂隙端部开始扩展至破裂。因此,脆性破坏不是因剪切而破坏,而是由于拉伸而破坏的。
具体准则(略)。
第四节 岩体的基本特征和类型
一、岩体的基本概念
第四节 岩体的基本特征和类型
二、岩体结构面及结构体特征
第四节 岩体的基本特征和类型
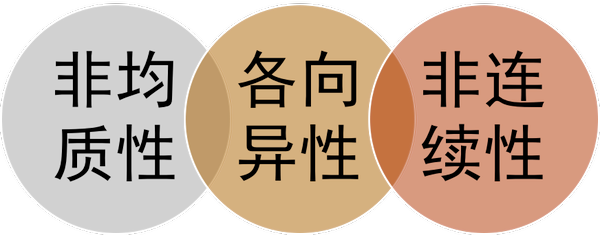
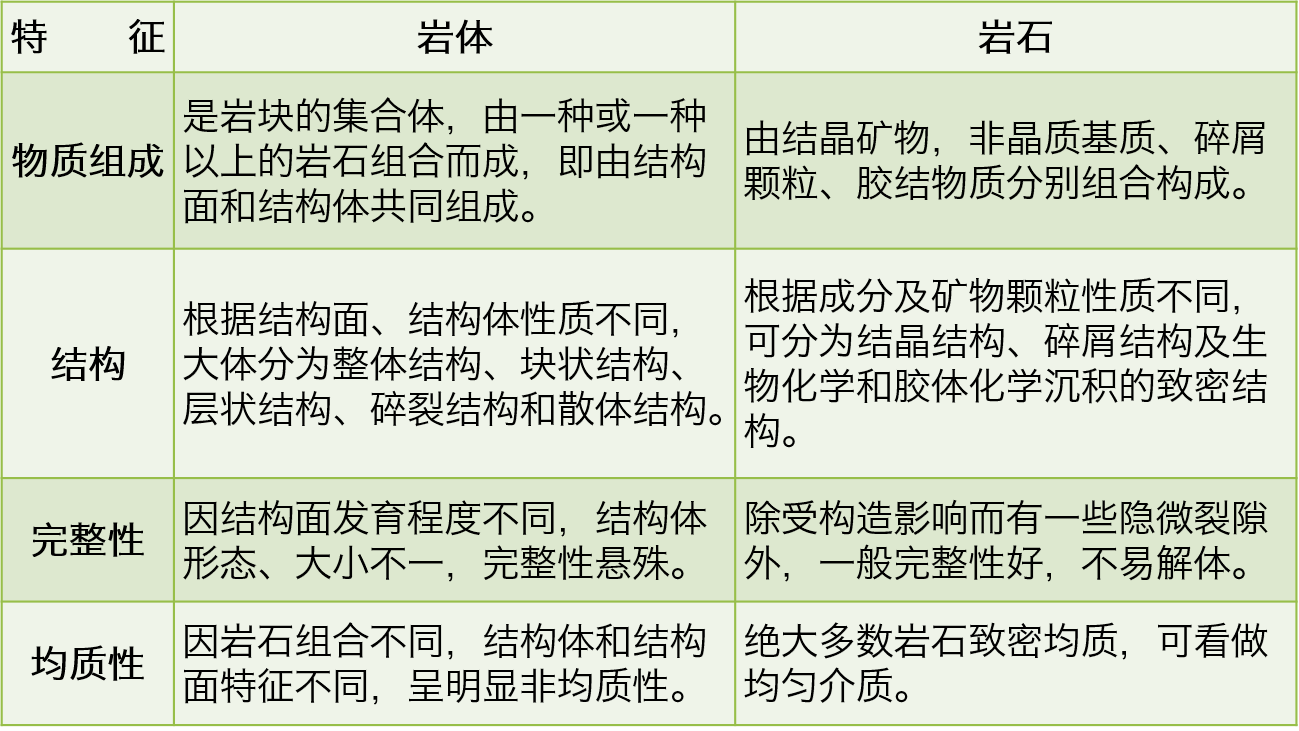
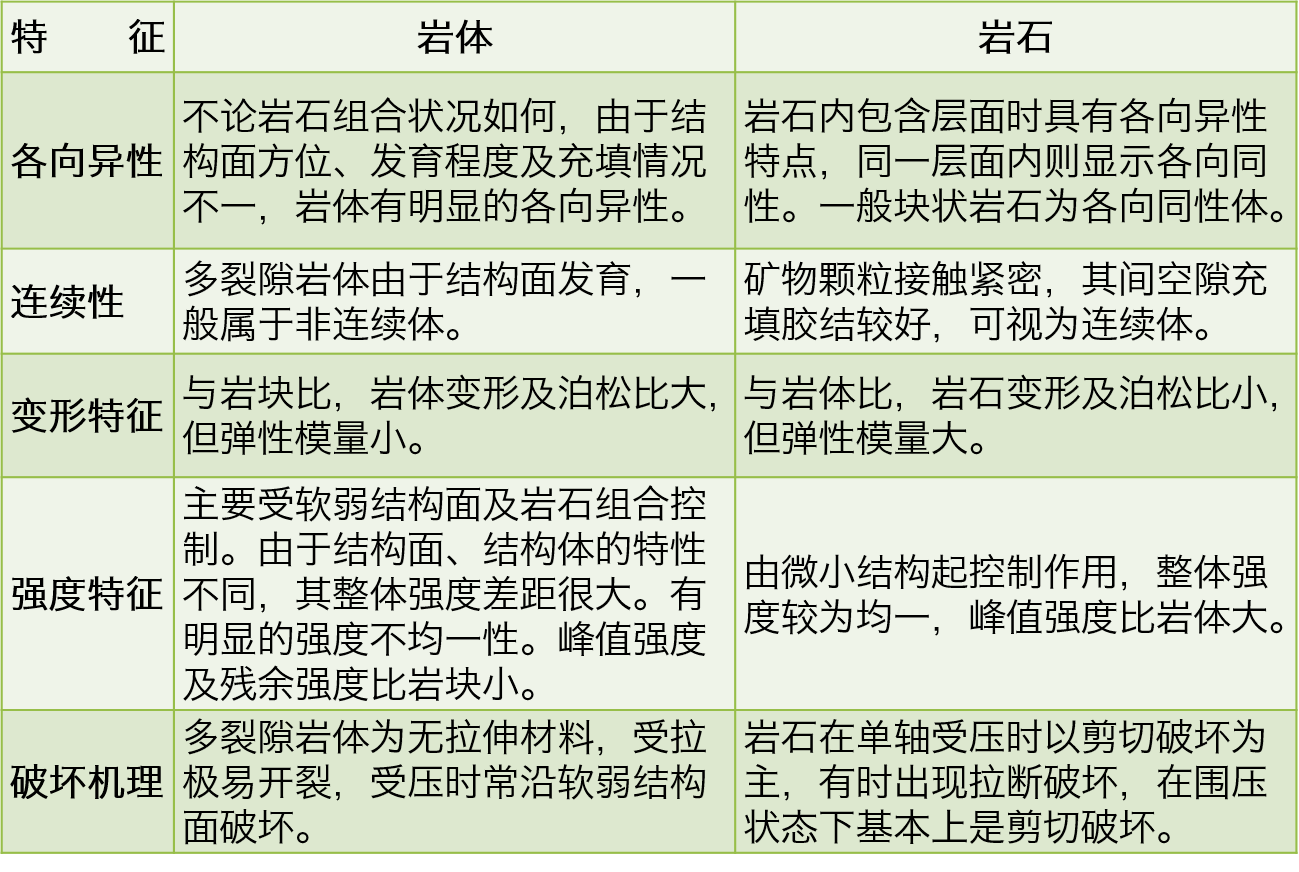
三、岩体的基本特征
第四节 岩体的基本特征和类型
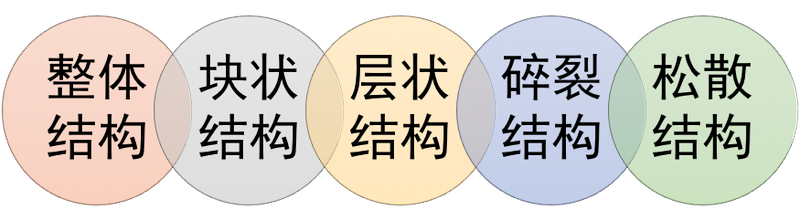
四、岩体结构的类型
第五节 岩体的基本力学性能与分级指标
一、岩体的变形特征
岩体的变形比岩石更加复杂。其总变形包括以压缩和形状变形为主的结构体变形及以压密和剪切滑移变形为主的结构面变形。此外,有的结构体在剪切过程中由于摩擦作用而发生转动。
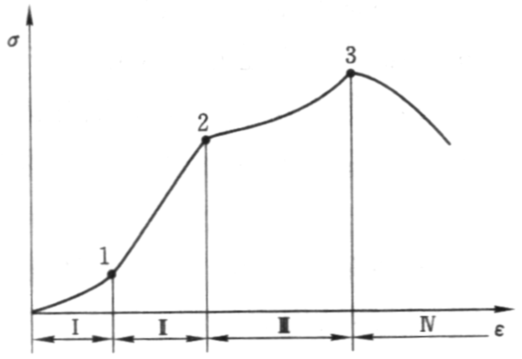
1—转化点;2—屈服点;3—极限强度
Ⅰ—压密阶段;Ⅱ—弹性阶段;Ⅲ—塑性阶段;Ⅳ—破坏阶段
第五节 岩体的基本力学性能与分级指标
二、岩体强度及其影响因素
岩体通常被看作是一种不抗拉材料。
大部分岩体在强度曲线的受压区仍符合莫尔—库伦准则。
学习要求
- 能说出 5 种以上煤矿常见岩石的名称。
- 了解岩石主要有哪些物理性质,各用什么指标进行表征?
- 掌握岩石三类变形性质的定义和区别,以及各类又包含哪些类型的变形特征。
- 理解岩石变形性质和强度性质的区别。
- 掌握岩石试件单轴受压时,其应力应变全程曲线的阶段划分及各阶段岩石的状态变化特征。
- 了解在不同的受载状态下,岩石强度大小的对比关系。
- 掌握岩石的破坏形式和破坏机理的分类方法。
- 掌握莫尔应力圆的画法,掌握极限应力圆、岩石强度曲线的概念,掌握摩尔—库伦强度准则公式及其图形表示。
- 了解格里菲斯强度理论中岩石破坏的机理。
- 掌握岩体和结构面的概念。
- 了解岩体的基本特征,了解岩石和岩体强度性质的不同点。
作 业
- 课本47页习题7:将某矿的页岩岩样做成5cm×5cm×5cm的三块立方体试件,分别做剪切角度为45°、55°和65°的抗剪强度试验,施加的最大载荷相应地为22.4kN、15.3kN、12.3kN,求该页岩的黏聚力C和内摩擦角φ值,并绘出该页岩的抗剪强度曲线图。
- 课本47页习题10:试作出单向拉伸、单向压缩、双向拉伸、双向压缩、双向不等拉压、纯剪、三向等拉、三向等压和三向不等压的应力圆(设压应力为正,σ1、σ2、σ3分别为最大、中间和最小主应力)。
- 课本47页习题13:在均质岩体中开一巷道,已知岩石的内摩擦角φ=30°,黏聚力C=40MPa,由实测知道巷道围岩所受平均铅直应力σ1=200MPa,这种情况下至少应对巷道边帮提供多大的侧向应力(σ3)才能维持巷道边帮的平衡?